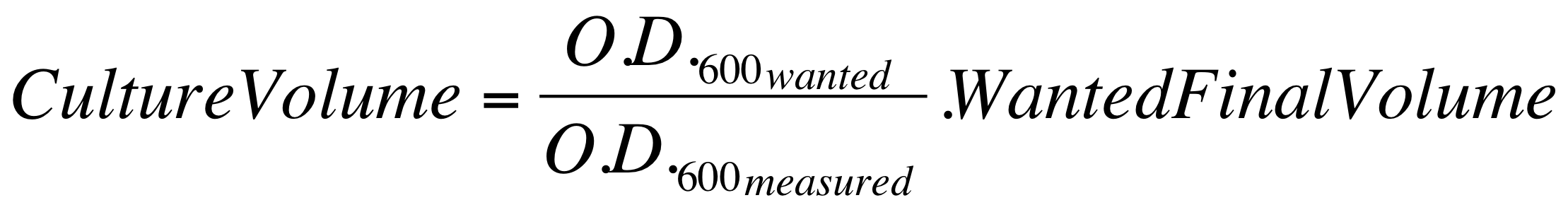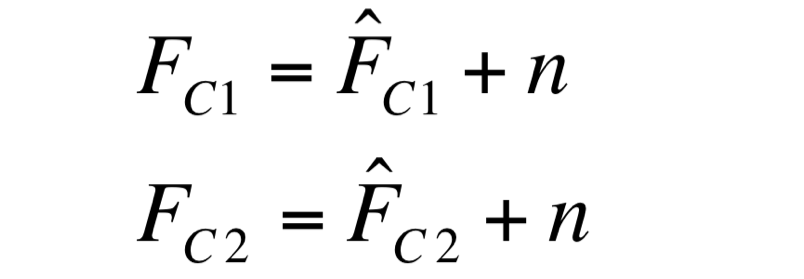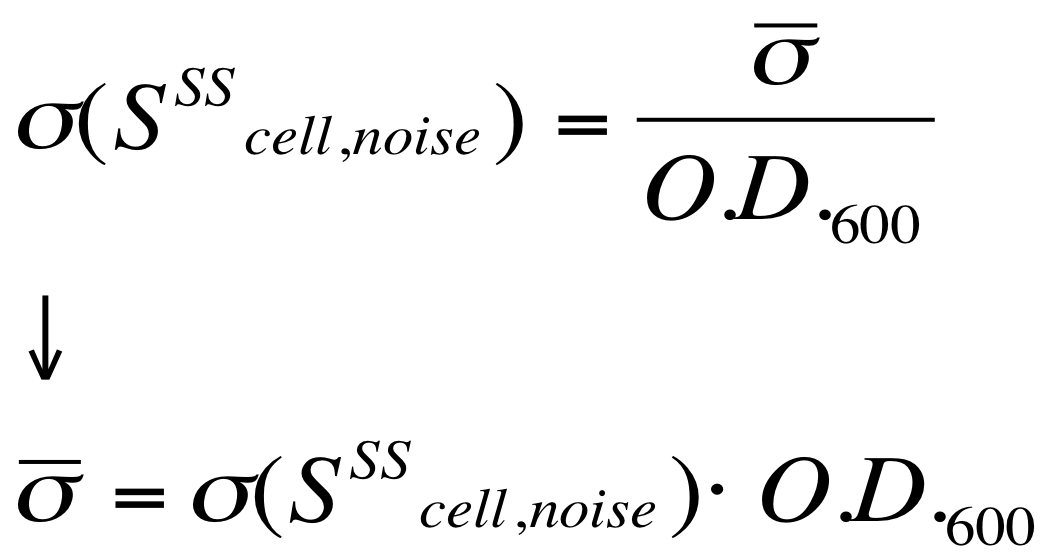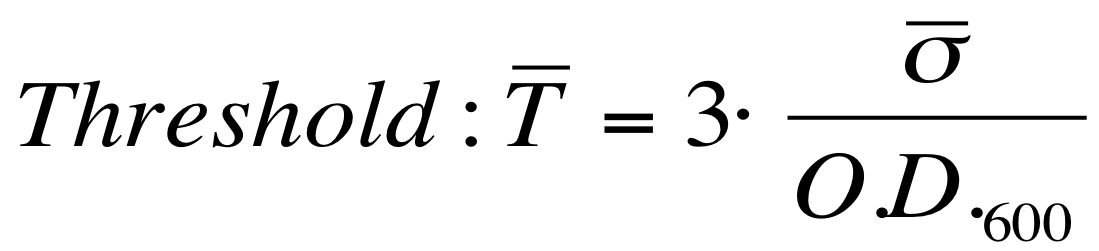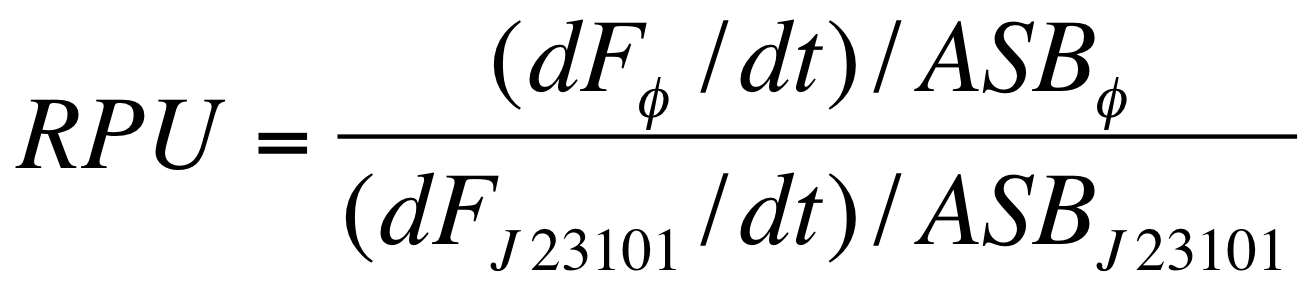|
CHARACTERIZATION
Growth conditions
Microplate reader experiments for self-inducible promoters - Protocol #1
- 8 ul of long term storage glycerol stock were inoculated in 1 ml of LB or M9 + suitable antibiotic in a 15 ml falcon tube and incubated at 37°C, 220 rpm for about 16 hours.
- The grown cultures were then diluted 1:100 in 1 ml of LB or M9 supplemented medium and incubated in the same conditions as before for about 4 hours.
- These new cultures were further grown for 4 hours (37 °C, 220 rpm) and then pelletted (2000 rpm, 10 minutes) in order to eliminate the HSL produced during the first growth.
- Supernatants were discarded and the pellets were resupsended in 1ml LB or M9 + suitable antibiotic and transferred to 1,5 ml Eppendorf tube
- Immediately, these cultures were diluted 1:1000 (1ul in 1ml LB or M9 + suitable antibiotic) and aliquoted in a flat-bottom 96-well microplate in triplicate, avoiding to perform dynamic experiments in the microplate frame (see Frame effect section – past year for details). All the wells were filled with a 200 ul volume.
- The microplate was incubated in the Tecan Infinite F200 microplate reader and fluorescence (when required) and absorbance were measured with this automatic protocol:
- 37°C constant for all the experiment;
- sampling time of 5 minutes;
- fluorescence gain of 50;
- O.D. filter was 600 nm;
- GFP filters were 485nm (ex) / 540nm (em);
- 15 seconds of linear shaking (3mm amplitude) followed by 10 seconds of waiting before the measurements in order to make a homogeneous culture.
- Variable experiment duration time (from 3 to 24 hours).
Microplate reader experiments for constitutive promoters (R.P.U. evaluation) - Protocol #2
- 8 ul of long term storage glycerol stock were inoculated in 5 ml of LB or M9 + suitable antibiotic in a 15 ml falcon tube and incubated at 37°C, 220 rpm for about 16 hours.
- The grown cultures were then diluted 1:100 in 5 ml of LB or M9 supplemented medium and incubated in the same conditions as before for about 4 hours.
- These new cultures were diluted to an O.D.600 of 0.02 (measured with a TECAN F200 microplate reader on a 200 ul of volume per well; it is not comparable with the 1 cm pathlength cuvette) in 2ml LB or M9 + suitable antibiotic. In order to have the cultures at the desired O.D.600, the following dilution was performed:
- These new dilutions were aliquoted in a flat-bottom 96-well microplate, avoiding to perform dynamic experiments in the microplate frame (see Frame effect section for details). All the wells were filled with a 200 ul volume.
- The microplate was incubated in the Tecan Infinite F200 microplate reader and fluorescence (when required) and absorbance were measured with this automatic protocol:
- 37°C constant for all the experiment;
- sampling time of 5 minutes;
- fluorescence gain of 50;
- O.D. filter was 600 nm;
- GFP filters were 485nm (ex) / 540nm (em);
- 15 seconds of linear shaking (3mm amplitude) followed by 10 seconds of waiting before the measurements in order to make a homogeneous culture.
- Experiment duration time (about 6 hours).
Data Analysis
- All our growth curves have been obtained subtracting for each time sample the broth O.D.600 measurement from that of the culture; broth was considered in the same conditions of the culture (e.g. induced with the same inducer concentration and supplemented with the same antibiotic of the culture).
- Fluorescence signals have been obtained subtracting for each time sample the fluorescent measurement of a non-fluorescent culture from that of the target culture. The non-fluorescent culture was considered in the same conditions of the target (e.g. induced with the same inducer concentration and with the BioBrick carried by the same plasmid, not encoding a fluorescent protein). This operation allows the removal, from the target fluorescent signal, of the "self-fluorescent" component and the fluorescence signal obtained is "blanked".
Doubling time evaluation
The natural logarithm of the growth curves (processed according to the above section) was computed and the linear phase (corresponding to the bacterial exponential growth phase) was isolated by visual inspection. Then the linear regression was performed in order to estimate the slope of the line m. Finally the doubling time was estimated as d=ln(2)/m [minutes].
In the case of multiple growth curves for a strain, the mean value of the processed curves was computed for each time sample before applying the above described procedure.
Data analysis for self-inducible promoters (initiation-treshold determination)
The task of our analysis is the evaluation of the initiation transcription point (in term of absorbance) for self-inducible devices. The transiction O.D.600 value is named, from now on, ODstart.
Data from three indipendent wells were averaged and blanked. O.D.600 signals were blanked as described in "Preliminary Remarks" section, while the fluorescence signal was blanked with the fluorescence of <partinfo>BBa_T9002</partinfo> part, assembled in the same plasmid of the considered promoter. This operation allows the removal from the fluorescence signal of the “self-fluorescent” component and of the “leaky ” component (due to the leakage of pLux in absence of the autoinducer molecule HSL).
ODstart was evaluated by computing the Scell signal for the desired self-inducible promoter and for the negative control.
Two different signals, measured from independent samples of the same non-fluorescent culture in the same experiment, are considered: C1 and C2. The fluorescence signal of C1 and C2 can be thought as the addition of a “real signal” and of a noise component.
since they are two time series acquired from the same culture, in the same growth condition by the same instrument.
F_C1 and F_C2 have the same expected value and the same standard deviation, since they are two independent realizations of the same aleatory process: in fact, they are two time series acquired from the same cultures, in the same growth conditions by the same instrument.
Noise signal was computed as:
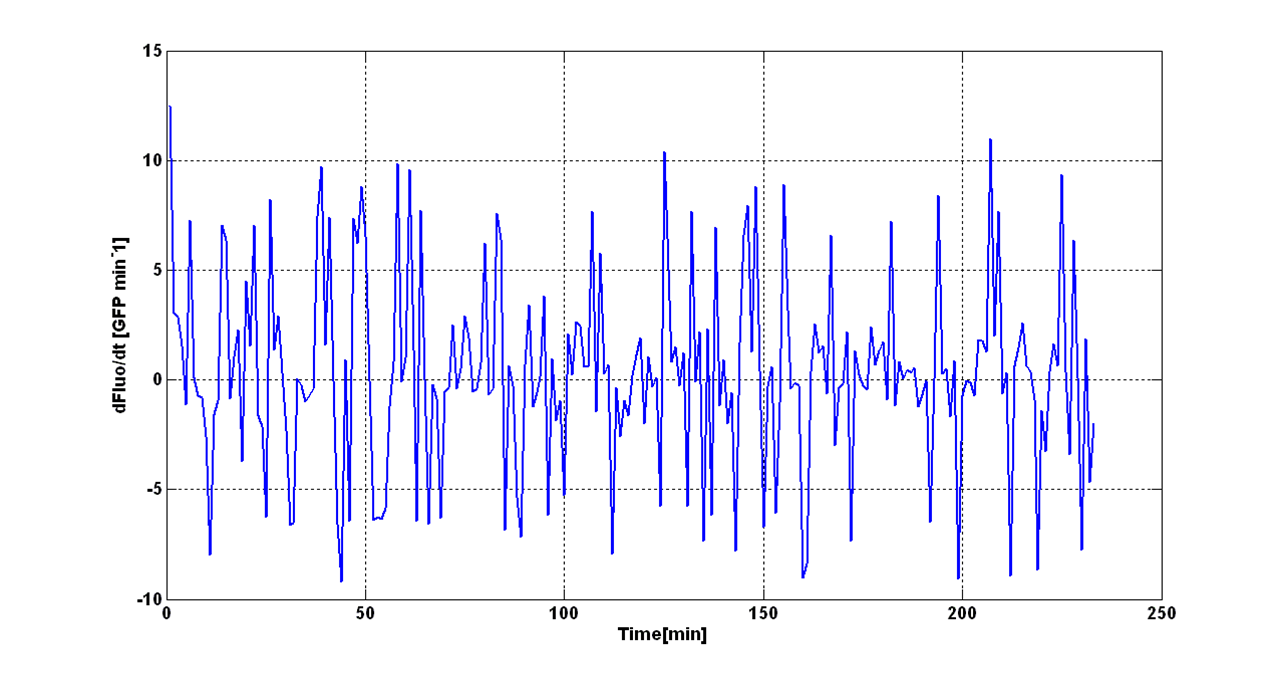
The behaviour of the signal N is shown in figure:
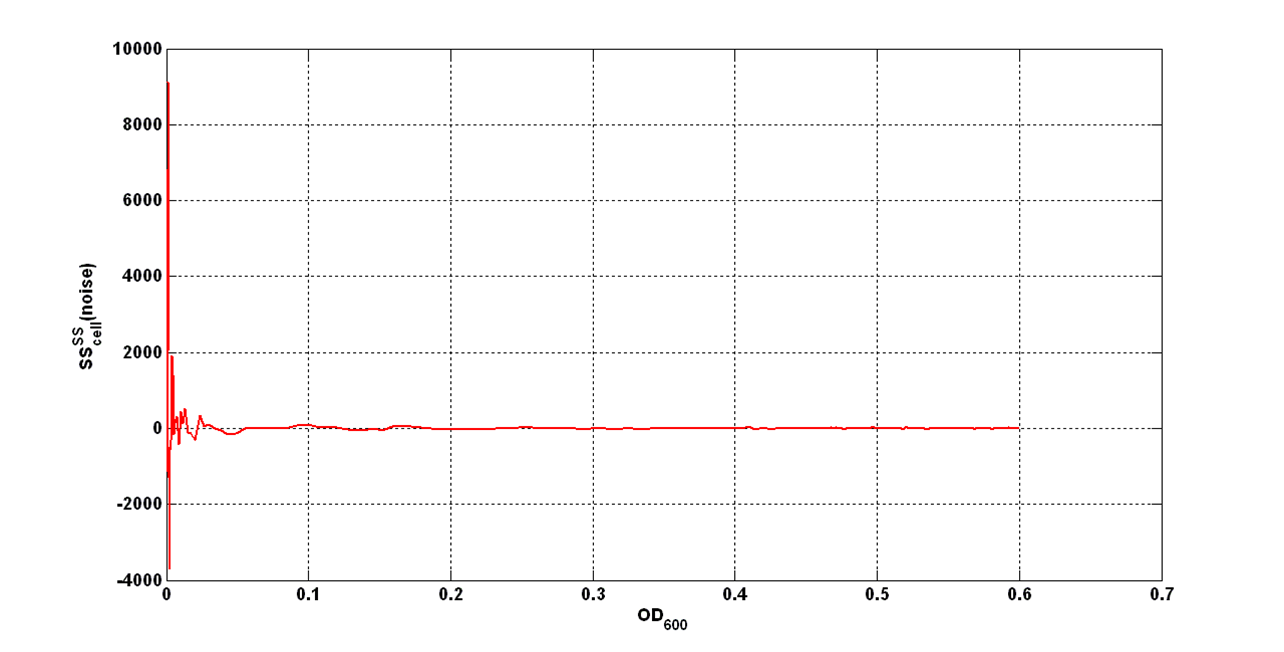
An interesting signal is Scell of N. It can be evaluated as the time derivative of N, divided by O.D.600 of the culture. It has the behaviour shown in figure:
It is fair to say that the noise of Scell is bigger for low O.D.600 values and its width decreases dramatically for higher O.D.600 values (e.g.: O.D.600>0,1 TECAN infinite F200).
The noise model proposed for the Scell noise signal is:
Once derived the noise of the Scell signal, the evaluation of the O.D.start can be performed supposing that the signal is significantly growing when at least 5 consecutive time samples exceed a threshold defined as follows:
The operation of subtracting the two signals F_C1 and F_C2 is analogous to the “blanking” operation performed on data, as described previously. For, this reason, under the hypothesis that the signals have the same variance (this is a consistent hypothesis, since they are measured by the same instrument in the same experimental conditions), this argument can be extended to the “blanked” data considered in the processing. Thus, this threshold was used to compute the O.D.start for the cultures. This heuristic algorithm was implemented in Matlab and analysis results are reported in the “results” section.
Data analysis for RPU evaluation
The RPUs are standard units proposed by Kelly J. et al., 2008, in which the transcriptional strength of a promoter can be measured using a reference standard.
RPUs have been computed as:
in which:
- phi is the considered promoter and J23101 is the reference standard promoter (taken from Anderson Promoter Collection);
- F is the blanked fluorescence of the culture, computed subtracting for each time sample fluorescence measure for negative control from that of culture, where the negative control is a non-fluorescent strain (in our experiment it is usually used TOP10 strain bearing BBa_B0032 or BBa_B0033, which are symmply RBSs do not have expression systems for reporter genes);
- ABS is the blanked absorbance (O.D.600) of the culture, computed as described in "Preliminary remarks" section.
RPU measurement has the following advantages (under suitable conditions)
- it is proportional to PoPS (Polymerase Per Second), a very important parameter that expresses the transcription rate of a promoter;
- it uses a reference standard and so measurements can be compared between different laboratories.
The hypotheses on which RPU theory is based can be found in Kelly J. et al., 2008, as well as all the mathematical steps. From our point of view, the main hypotheses that have to be satisfied are the following
- the reporter protein must have a half life higher than the experiment duration (we use GFPmut3, BBa_E0240, which has an estimated half life of at least 24 hours, and the experiments duration is always less than 7 hours);
- strain, plasmid copy number, antibiotic, growth medium, growth conditions, protein generator assembled downstream of the promoter must be the same in the promoter of interest and in J23101 reference standard.
- steady state must be valid, so (dF/dt)/ABS (proportional to the GFP synthesis rate per cell) must be constant.
In order to compute the RPUs, the Scell signals ((dGFP/dt)/ASB)) of the promoter of interest and of the reference J23101 were averaged in the time interval corresponding to the exponential growth phase. The boundaries of exponential phase were identified with a visual inspection of the linear phase of the logarithmic growth curve.
|
 "
"