"

From 2010.igem.org

Revision as of 16:48, 23 October 2010 (view source) Seongkyu (Talk | contribs) (→Surface Display) ← Older edit		Revision as of 16:48, 23 October 2010 (view source) Seongkyu (Talk | contribs) (→Surface Display) Newer edit →
Line 113:		Line 113:
	<br style="clear: both" />		<br style="clear: both" />
-	[[Image:flocculation1.jpg|left|460px|thumb|fig.1 Hello, this is testing!]][[Image:flocculation1.jpg|right|460px|thumb|fig.2 put another descrip.]]	+	[[Image:flocculation1.jpg|left|455px|thumb|fig.1 Hello, this is testing!]][[Image:flocculation1.jpg|right|455px|thumb|fig.2 put another descrip.]]
	<br style="clear: both" />		<br style="clear: both" />

---

Revision as of 16:48, 23 October 2010

Mathematical models are very important in the design of an iGEM project. The Michigan modeling team is composed of Josh, Kevin, Candy, Jennifer, and John. We are currently researching different models that have been previously done that can help us in our own modeling endeavors. To construct our models, we have taken advantage of MATLAB's Simbiology toolset. More information and tutorials on Matlab and Simbiology can be found here: [http://www.mathworks.com/academia/student_center/tutorials/launchpad.html?s_cid=0410_webg_igem10_294031 MATLAB Tutorial]

There are several components to a good mathematical model. These include assumptions, parameters, and equations.

Pili

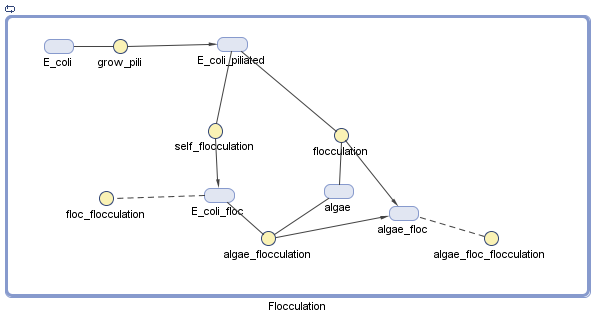
We have decided to model the growth of a biofilm using pili. By modeling the flocculation of the algae, we hope to be able to predict how our reactions will proceed and determine quantities such as the optimal initial concentration of E. coli.

Assumptions
There is no growth or degradation of cells and algae.

• I made this assumption to simplify the model.

Floc formation only involves two particles. Collision efficiency is perfect.

• This assumption greatly simplifies the model.

Parameters
All rate constants set to 0.1.

• This is obviously unrealistic, but with experimental data, we can refine the numbers.

Initial quantities of E. coli and algae are 1 mol.

• We can perform assays to determine the ideal starting conditions.

Quorum Sensing

Quorum sensing has been modeled by other iGEM teams for previous competitions, including: [http://parts.mit.edu/igem07/index.php/Bangalore Bangalore] and Singapore

This model is based on the paper [http://jb.asm.org/cgi/content/short/189/16/6011 Quorum Sensing in Escherichia coli Is Signaled by AI-2/LsrR: Effects on Small RNA and Biofilm Architecture (doi:10.1128/JB.00014-07)] and was created with the help of Alex who is also on the quorum sensing team. More information about quorum sensing can be found here: Team:Michigan/Project and their notebook can be found here: Team:Michigan/Quorum_Sensing.

This model shows the movement of AI2 (Autoinducer-2) from outside the cell (AI2_o) to inside the cell (AI2_i). The final output after transcription and translation is GFP in the case of the Lux- mutants recieved; however, at the end of the project, this will hopefully cause flocculation of the microalgae.

This model is also specific to the Lux- mutants as it is not understood how LuxS works or is produced. [http://jb.asm.org/cgi/content/short/189/16/6011 (doi:10.1128/JB.00014-07)]

Assumptions

• Assume all massaction
  • This greatly simplifies the model and gives a good estimate; however, it is unrealistic.
• Initially, all LsrR bound to all operators to inhibit.
  • This also simplifies the model.
• Creation of LsrS is unknown so simply exists in the cell at a fixed concentration. Any output that occurs is due to the addition of AI2 from the person performing the experiment.
• Assume that the proteins that bring in AI2 (Lsr A, B, C, and D) exist in a protein complex and can be called one "species" in Matlab. Also assume that the protein complex is created and formed at the same time.
  • This simplifies the number of species in Matlab and also simplifies the model.
• Assuming no degradation for now... Molecule is "used" up in reaction.
  • This simplifies the model by removing degradation from the equations.

Parameters

• For now, all rate constants are 1.
  • This simplifies the model; however, it is not realistic.
• Assumptions with quantities
  • A lot of AI2_o in comparison with all other molecules.
    • This is saying that the experimenter will add a higher concentration of AI2 than the concentrations of various molecules that exist in the cell.
  • Initially low concentration of Lsr A,B,C,D transport proteins
    • Low basal expression of the transport proteins.
  • Low concentration of LsrK
    • Low basal expression of LsrK.
  • Low concentration of LsrR + Operator
    • In comparison with the protein concentration, the number of plasmids containing the Operator is low.

GFP Output

Since the Quorum Sensing Team is only measuring the output of GFP from the addition of AI2, this is the output that really matters. As can be seen, after a certain amount of time, the expression of GFP levels off.

Surface Display

This model predicts the behavior of an algae specific binding protein expressed by E. Coli. It is relevant to vp130 project described here.

Assumptions

1-1. The flocculation depends on only the concentrations of algae and flocculant.

1-2. The flocculation depends on only the collision between species with surface proteins and algae

2. The forward reaction for flocculation is much faster than the reverse reaction.

3-1. Flocculated species are invincible--they do not die.

3-2. Other species, such as unexpressed/expressed species and algae, also do not die.

• Our model takes into account the deaths for all the species mention above, but the constants were made not functional during the simulation.

4. Algae and unexpressed/expressed species are assumed to grow on the same media.

• However, if necessary, our model can assume that they grow on separate media and then added together to flocculate.

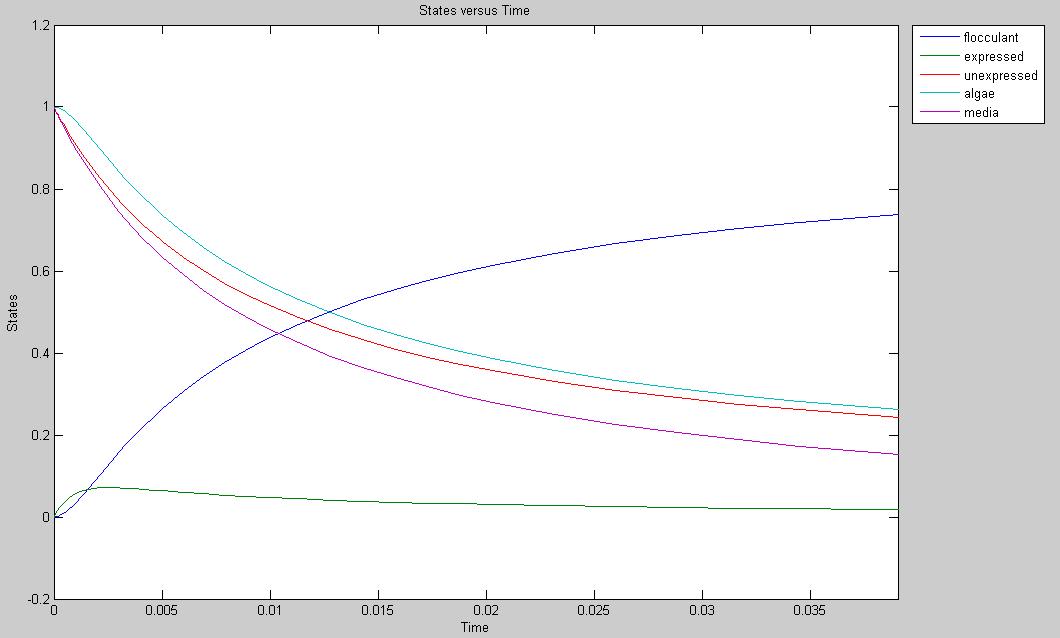
5. The expression of surface proteins is based on solely the amount of "unexpressed" species and the concentration of media.

Parameters

1. Significant rate constants

• Forward flocculation: 1000.0 / (mol x sec)
• Reverse flocculation: 1.0 / (sec)
• Surface protein expression: 100.0 / (mol x sec)

2. Initial concentrations

• Media: 1 mol
• Unexpressed species: 1 mol
• Algae: 1 mol

Oil Sands

We are developing a mathematical model which describes the degradation of naphthenic acids (NAs) by Pseudomonas putida and Pseudomonas fluorescens in a biofilm in a drip flow bioreactor under aerobic conditions. We will use a series of [http://controls.engin.umich.edu/wiki/index.php/Bacterial_Chemostat_Model chemostat] models to approximate the change in NA concentration along the length of the bioreactor and through time.

In developing the mathematical model, we made the following assumptions:

• Our models will assume a homogeneous mixture of P. putida and P. fluorescens and represent the two species as one organism.
  • It is known that P. putida and P. fluorescens synergistically degrade NAs [4]. The mechanism of the synergistic degradation and differentiation between the two species should have little effect in evaluating the efficiency of NA degradation.

• The biofilm is always distributed homogeneously throughout the bioreactor, and diffusion of NAs into the biofilm occurs instantaneously.
  • This assumption is made to simplify the model.

• We assume that NAs remain in solution within the bioreactor.
  • NAs are not known to be volatile.

• The density ratio of the two Pseudomonas species do not fluctuate.
  • This assumption is likely unrealistic.

• Oxygen is not a limiting substrate.

• Area of cross sections remain unchanged through the length of bioreactor.

Reactions

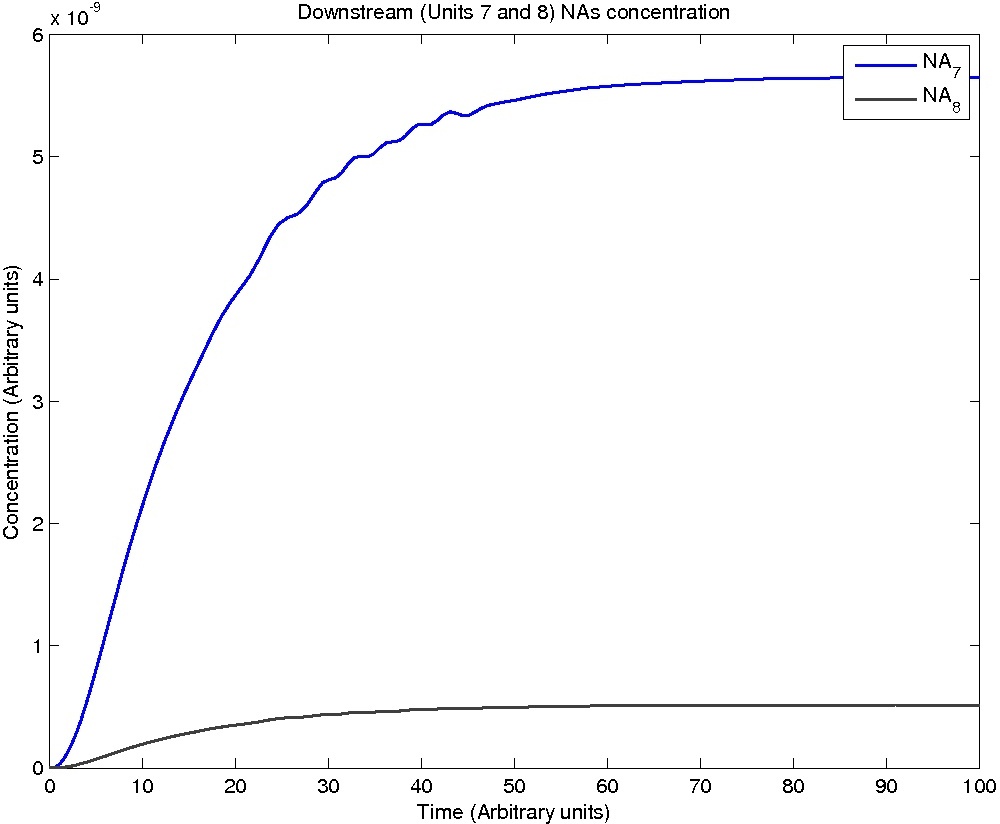
The system is represented by nine repeating units of the following reactions, with the units distinguished by a number n: 0 =< n =< 8. All reactions are assumed to be mass action. For n = 0, there is no NA_n-1 -> NA_n and NA_n is a constant.

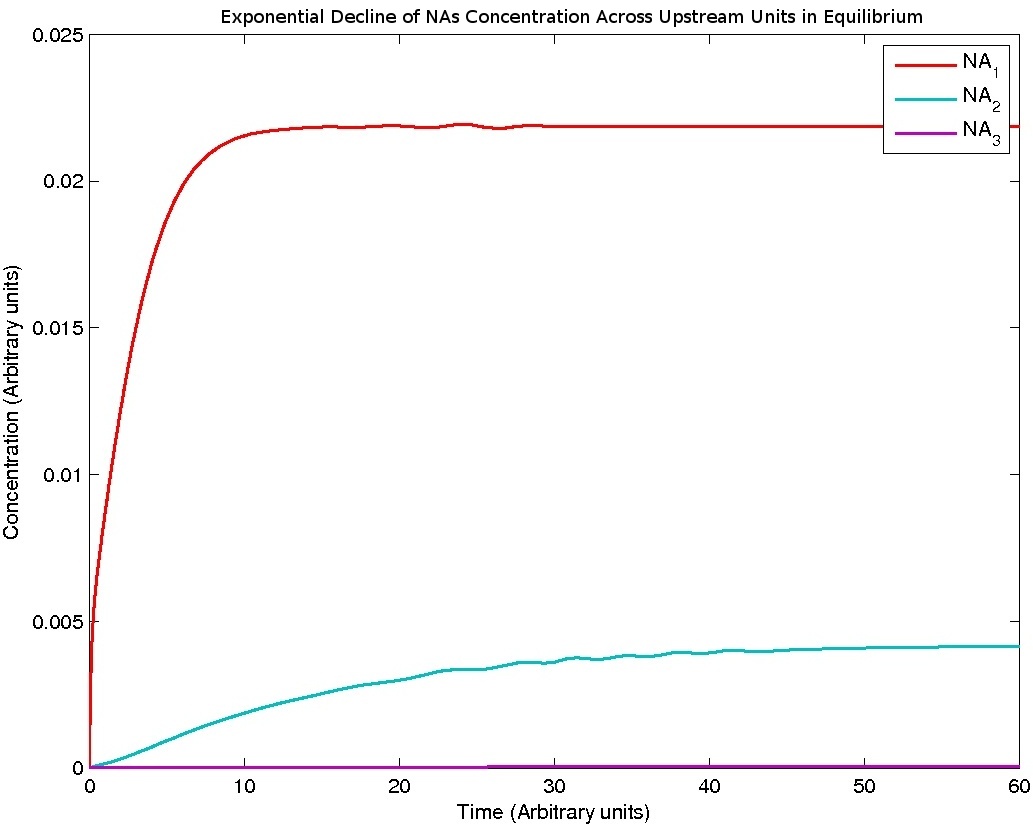
The flow of NA from one unit to the next is described simply with a mass action model:

dNA_n = kinflow_n-1*NA_n-1 - kinflow_n*NA_n

As the velocity of the liquid is constant throughout the model, kinflow_n-1 = kinflow_n.

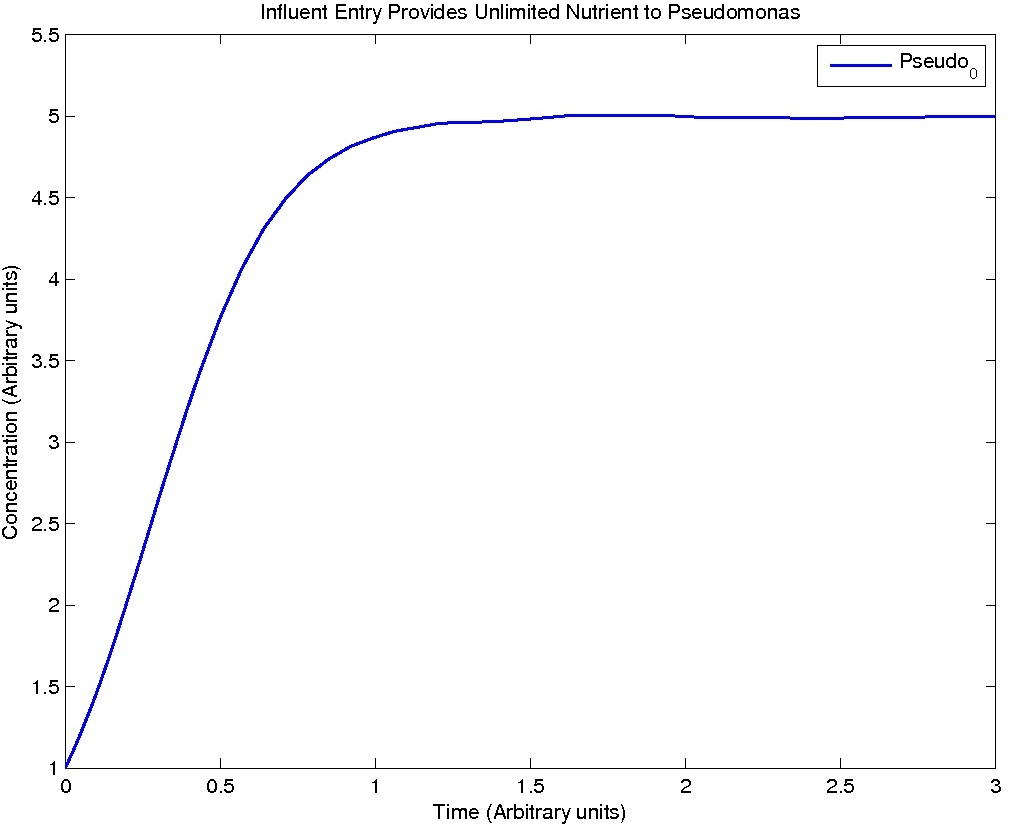
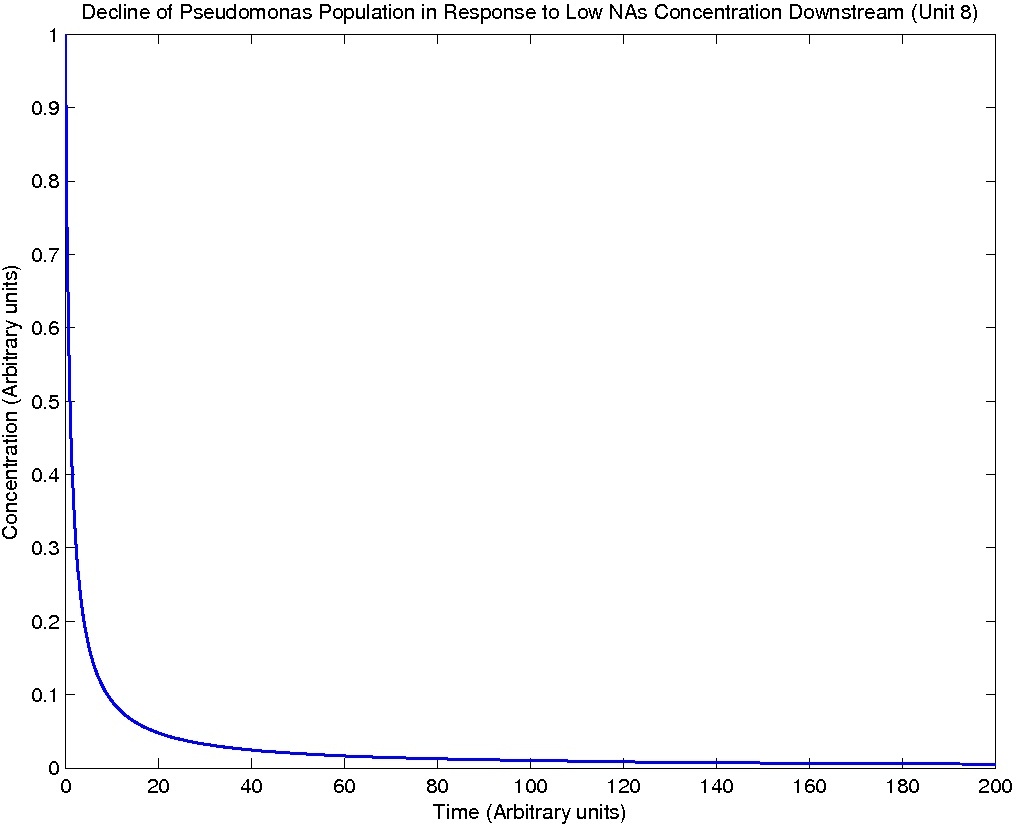
Pseudomonas population is modeled by the logistic growth curve, yielding

 dPseudo_n/dt = kdegrade*NA_n*Pseudo_n - kdeath*(Pseudo_n)^2

Rate:	Value:
kinflow	0.1
kdegrade	10.0
kdeath	1.0

Initial value:	Note:	Value:
NA_0	A constant	0.5
NA_n	n > 0	0.0
Pseudo_n		1.0

Results

Note: Although concentration and time are in arbitrary units, they are consistent across all plots.

Ideally, a drip flow bioreactor should be modeled by a plug flow reactor model, which describes a fluid flowing through a pipe with perfect mixing in the radial direction and no mixing in the axial direction. However, we deemed the method above to be sufficient for our purposes and more intuitive in design. uOttawa used plug flow model to describe nutrient flow in the intestines.

References

1. Kuwahara, H., Myers, C., Samoilov, M., Abstracted Stochastic Analysis of Type 1 Pili Expression in E. Coli.

2. [http://jb.asm.org/cgi/content/short/189/16/6011 Li, J., C. Attila, L. Wang, T. K. Wood, J. J. Valdes, and W. E. Bentley. 2007. Quorum sensing in Escherichia coli is signaled by AI-2/LsrR: effects on small RNA and biofilm architecture. J. Bacteriol. 189:6011-6020.]

3. Wolf, D., and Arkin, A., Fifteen Minutes of fim: Control of Type 1 Pili Expression in E. Coli. OMICS 6 2002

4. [http://www.ncbi.nlm.nih.gov/pubmed/17040229 Del Rio, L., Hadwin, A., Pinto, L., MacKinnon, M. and Moore, M. (2006), Degradation of naphthenic acids by sediment micro-organisms. Journal of Applied Microbiology, 101: 1049–1061.]