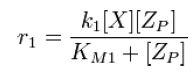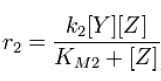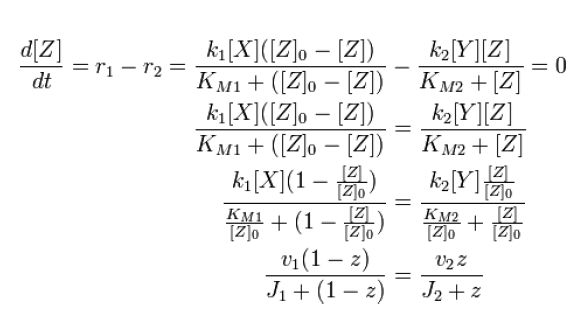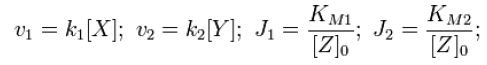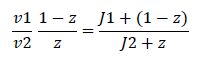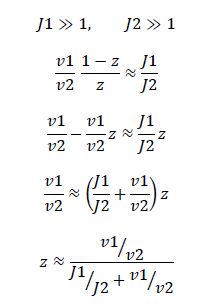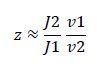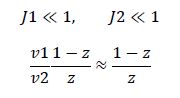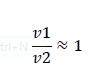Team:Stanford/Research/Modeling

From 2010.igem.org

(Difference between revisions)
(→Kinase/Phosphatase System)
 
(23 intermediate revisions not shown)
Line 5: Line 5:
Our intuition for what makes a good ratio sensor could only take us so far.  From the very first stages of design, we wanted to back up and test our ideas with mathematical tools.  Luckily, we found that solving the equations of mass action kinetics at steady-state was enough to give us clear design criteria.  We present the mathematical basis for sensors that are capable of sensing a single ratio digitally, or many ratios in an analog fashion.
Our intuition for what makes a good ratio sensor could only take us so far.  From the very first stages of design, we wanted to back up and test our ideas with mathematical tools.  Luckily, we found that solving the equations of mass action kinetics at steady-state was enough to give us clear design criteria.  We present the mathematical basis for sensors that are capable of sensing a single ratio digitally, or many ratios in an analog fashion.
-
==The System==
+
==Kinase/Phosphatase System==
 +
Throughout this derivation, we refer to Goldbeter and Koshland's seminal work on the kinetics of emzyme pairs [[Team:Stanford/Research/Modeling#References| [1]]].
 +
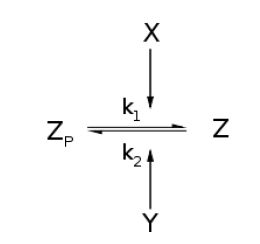
For an opposing pair of enzymes ''X'' and ''Y'' modifying and unmodifying a substrate ''Z'' with modification ''p'',
 +
[[Image:MainGBK.JPG|center]]
 +
From Michaelis-Menten kinetics we know that the rate at which ''Zp'' is dephosphorylated is
 +
[[Image:R1.JPG]][[Team:Stanford/Research/Modeling#References| [2]]]
-
===sRNA System===
+
and the rate at which ''Z'' is phosphorylated is
-
Boolean model for the sRNA system. This is mean to provide a significantly simplified mathematical understanding of the dynamics involved.
+
[[Image:R2.JPG]][[Team:Stanford/Research/Modeling#References| [2]]]
-
<html>
+
We also know that ''Z'' can be modified an unmodified, but its total is conserved: ''[Z]o = [Zp] + [Z]''
-
<head>
+
-
      <meta http-equiv="Content-Type" content="text/html; charset=utf-8">
+
-
  <!--
+
-
This HTML is auto-generated from an M-file.
+
-
To make changes, update the M-file and republish this document.
+
-
      --><title>iGEM_boolean_sRNA_model</title><meta name="generator" content="MATLAB 7.10"><meta name="date" content="2010-10-27"><meta name="m-file" content="iGEM_boolean_sRNA_model"><style type="text/css">
+
-
body {
+
At steady state, modification and unmodification rates are equal, leading us to
-
  background-color: white;
+
-
  margin:10px;
+
-
}
+
-
h1 {
+
[[Image:1stblock.JPG]][[Team:Stanford/Research/Modeling#References| [2]]]
-
  color: #990000;
+
-
  font-size: x-large;
+
-
}
+
-
h2 {
+
where
-
  color: #990000;
+
-
  font-size: medium;
+
-
}
+
-
/* Make the text shrink to fit narrow windows, but not stretch too far in
+
[[Image:2nd_block.JPG]][[Team:Stanford/Research/Modeling#References| [2]]]
-
wide windows. */
+
-
p,h1,h2,div.content div {
+
-
  max-width: 600px;
+
-
  /* Hack for IE6 */
+
-
  width: auto !important; width: 600px;
+
-
}
+
-
pre.codeinput {
 
-
  background: #EEEEEE;
 
-
  padding: 10px;
 
-
}
 
-
@media print {
 
-
  pre.codeinput {word-wrap:break-word; width:100%;}
 
-
}
 
-
span.keyword {color: #0000FF}
+
Rearranging gives
-
span.comment {color: #228B22}
+
-
span.string {color: #A020F0}
+
-
span.untermstring {color: #B20000}
+
-
span.syscmd {color: #B28C00}
+
-
pre.codeoutput {
+
[[Image:3rdblock.JPG|center]]
-
  color: #666666;
+
-
  padding: 10px;
+
-
}
+
-
pre.error {
+
Now, assume that the two opposing enzymes are nowhere near being saturated with substrate:
-
  color: red;
+
-
}
+
-
p.footer {
+
[[Image:4thblock.JPG|center]]
-
  text-align: right;
+
-
  font-size: xx-small;
+
-
  font-weight: lighter;
+
-
  font-style: italic;
+
-
  color: gray;
+
-
}
+
-
  </style></head><body><div class="content"><pre class="codeinput">clear <span class="string">all</span>
+
which is the equation for a Michaelis-Menten-shaped curve as shown below:
-
clc
+
-
<span class="comment">%Constants and Values</span>
+
[[Image:Langmuir.JPG|center]]
-
trackingNum = 6;    <span class="comment">%mRNA_pA, mRNA_pB, sRNA_A, sRNA_B, protein_A, protein_B;</span>
+
-
inputNum = 2;      <span class="comment">%A, B;</span>
+
-
processNum = 6;    <span class="comment">%Trx_pA, Trx_sRNA_A, Trx_pB, Trx_sRNA_B, Trl_A, Trl_B;</span>
+
-
<span class="comment">%Cell/Matrix Dimensions</span>
+
So, the fraction of modified substrate is a saturating function of the ratio of inputs, the half-max value is the ratio of the strengths of the two enzymes, and the fraction of unmodified substrate is a linear function of the ratio of inputs,
-
m = 2^trackingNum;
+
-
n = 2^inputNum;
+
-
c = cell(m+1, n+1);
+
-
trackingMatrix = de2bi(0:m-1);
+
[[Image:6thblock.JPG|center]]
-
inputMatrix = de2bi(0:n-1);
+
-
processMatrix = zeros(1,processNum);
+
-
<span class="comment">%Populating the Cell (Tracking x Input)</span>
+
We now know that the requirements for this analog ratio sensor are
-
c{1,1} = [0];
+
<ol>
-
<span class="keyword">for</span> j = 1
+
<li>Consistent relationships between inputs and enzyme activities (non-trivial)</li>
-
    <span class="keyword">for</span> i = 2:m+1
+
<li>A non-saturating amount of substrate</li>
-
        c{i,j} = trackingMatrix(i-1,:);
+
</ol>
-
    <span class="keyword">end</span>
+
-
<span class="keyword">end</span>
+
-
<span class="keyword">for</span> i = 1
+
-
    <span class="keyword">for</span> j = 2:n+1
+
-
        c{i,j} = inputMatrix(j-1,:);
+
-
    <span class="keyword">end</span>
+
-
<span class="keyword">end</span>
+
-
<span class="keyword">for</span> i = 2:m+1
+
-
    <span class="keyword">for</span> j = 2:n+1
+
-
        c{i,j} = processMatrix;
+
-
    <span class="keyword">end</span>
+
-
<span class="keyword">end</span>
+
-
<span class="comment">%Rules, Acessing, and Changing</span>
+
But what happens if we disobey requirement 1?  Let's increase the amount of substrate to saturation so that
-
<span class="keyword">for</span> j = 2:n+1
+
-
    A = c{1,j}(1);
+
-
    B = c{1,j}(2);
+
-
    <span class="keyword">for</span> i = 2:m+1
+
[[Image:7thblock.JPG|center]]
-
        mRNA_pA = c{i,1}(1);
+
-
        mRNA_pB = c{i,1}(2);
+
-
        sRNA_A = c{i,1}(3);
+
-
        sRNA_B = c{i,1}(4);
+
-
        protein_A = c{i,1}(5);
+
-
        protein_B = c{i,1}(6);
+
-
        <span class="comment">%Trx_pA</span>
+
[[Image:8thblock.JPG|center]]
-
        <span class="keyword">if</span> A == 1
+
-
            c{i,j}(1) = 1;
+
-
        <span class="keyword">end</span>
+
-
        <span class="comment">%Trx_pB</span>
+
When the enzymes are saturated, the only steady-state solution is'' v1'' = ''v2''.  Any ratio of ''v1/v2'' below this, and all the substrate becomes modified.  Any ratio above and all the substrate becomes unmodified.  Simply by changing the concentration of substrate, we have converted our analog ratio sensor to a digital ratio sensor.
-
        <span class="keyword">if</span> B == 1
+
-
            c{i,j}(2) = 1;
+
-
        <span class="keyword">end</span>
+
-
        <span class="comment">%Trx_sRNA_A</span>
+
The requirements for this digital ratio sensor are:
-
        <span class="keyword">if</span> A == 1
+
<ol>
-
            c{i,j}(3) = 1;
+
<li>Consistent relationships between inputs and enzyme activities (non-trivial)</li>
-
        <span class="keyword">end</span>
+
<li>An amount of substrate sufficient to saturate both opposing enzymes</li>
 +
</ol>
-
        <span class="comment">%Trx_sRNA_B</span>
+
==sRNA System==
-
        <span class="keyword">if</span> B == 1
+
This sRNA system is bases its analysis on the work of Nicolas Buchler. [[Team:Stanford/Research/Modeling#References| [3]]]
-
            c{i,j}(4) = 1;
+
-
        <span class="keyword">end</span>
+
-
        <span class="comment">%Trl_A</span>
+
Consider an sRNA that can bind to an mRNA and inhibit its translation.  The pair binds and dissociates with dissociation constant Kd. 
-
        <span class="keyword">if</span> mRNA_pA == 1 &amp;&amp; mRNA_pB == 0
+
-
            c{i,j}(5) = 1;
+
-
        <span class="keyword">end</span>
+
-
        <span class="comment">%Trl_B</span>
+
For a moment, imagine that this interaction is infinitely strong, such that Kd -> 0.  In this case, all the mRNA available will bind to the sRNA, until every sRNA is occupied by one mRNA.  Once this threshold, defined by the total sRNA concentration, is reached, additional mRNA added is free to be translated.  Here we show the accumulation of translatable free mRNA, and hence Gene Expression vs. total mRNA, in the presence of varying concentrations of infinitely strong sRNA
-
        <span class="keyword">if</span> mRNA_pB == 1 &amp;&amp; mRNA_pA == 0
+
-
            c{i,j}(6) = 1;
+
-
        <span class="keyword">end</span>
+
-
    <span class="keyword">end</span>
+
[[Image:sRNA1.JPG|center]]
-
<span class="keyword">end</span>
+
-
<span class="comment">%Display Results (Column by Column)</span>
+
At the point that the sRNA becomes saturated, two interesting things occur. 
-
[nrows,ncols]= size(c);
+
<ol>
-
<span class="comment">%Condense Cell and Display</span>
+
<li>There is a sharp transition between no gene expression and a linearly-increasing amount of gene expression.</li>
-
<span class="keyword">for</span> i = 1:nrows
+
<li>This transition occurs only when the concentration of mRNA is equal to the concentration of sRNA.</li>
-
    <span class="keyword">for</span> j = 1:ncols
+
</ol>
-
        string = num2str(c{i,j});
+
-
        l = length(string);
+
-
        r = 1;
+
-
        s = 1;
+
-
        t = 0;
+
-
        <span class="keyword">while</span> t ~= 1
+
We have designed a sensor that responds to a 1:1 mRNA:sRNA ratio with a sharp change in output.
-
            <span class="keyword">if</span> r == l
+
-
            t = 1;
+
-
            <span class="keyword">end</span>
+
-
            noSpacesString(s) = string(r);
+
But will this system have the same desirable properties when the sRNA is only realistically strong?  Here we assume a 1 nM interaction between sRNA and mRNA
-
            r = r+3;
+
-
            s = s+1;
+
-
        <span class="keyword">end</span>
+
-
        c{i,j} = noSpacesString;
+
-
    <span class="keyword">end</span>
+
-
<span class="keyword">end</span>
+
-
c(:,:)
+
-
<span class="comment">%Find Steady States and Corresponding Inputs</span>
+
[[Image:sRNA2.JPG|center]]
-
counter = 1;
+
-
<span class="keyword">for</span> i = 2:m+1
+
-
    <span class="keyword">for</span> j = 2:n+1
+
-
        <span class="keyword">if</span> c{i,j} == c{i,1}
+
-
            completeMatrix{counter,1} = c{i,j};            <span class="comment">%Steady state values</span>
+
-
            completeMatrix{counter,2} = num2str([i-1,j-1]); <span class="comment">%Location (n x m) within results area</span>
+
-
            completeMatrix{counter,3} = c{1,j};            <span class="comment">%Corresponding input values</span>
+
-
            counter = counter+1;
+
-
        <span class="keyword">end</span>
+
-
    <span class="keyword">end</span>
+
-
<span class="keyword">end</span>
+
-
SS_mXn_Input = completeMatrix
+
-
time = 0:processNum;
+
We find that the transition is still quite sharp when the sRNA has a realistic dissociation constant.
-
<span class="comment">%plot(time,,time,,time,,time,,time,,time,)</span>
+
-
<span class="comment">%New Cell for Specific Cases</span>
+
== References ==
-
<span class="comment">% d(:,1) = c(:,1);</span>
+
[1] [http://www.ncbi.nlm.nih.gov/pubmed/6947258 Goldbeter A, Koshland DE Jr.: An amplified sensitivity arising from covalent modification in biological systems. PNAS. 1981 Nov; 78(11) 6840-4.]
-
<span class="comment">% for j = 2:n+1</span>
+
-
<span class="comment">%    C1 = '0000';</span>
+
-
<span class="comment">%    C2 = '0011';</span>
+
-
<span class="comment">%    C3 = '0100';</span>
+
-
<span class="comment">%    C4 = '0111';</span>
+
-
<span class="comment">%    C5 = '1000';</span>
+
-
<span class="comment">%    C6 = '1011';</span>
+
-
<span class="comment">%    C7 = '1100';</span>
+
-
<span class="comment">%</span>
+
-
<span class="comment">%    a = {C1, C2, C3, C4, C5, C6, C7};</span>
+
-
<span class="comment">%    for b = 1:1:length(a)</span>
+
-
<span class="comment">%        if strcmp(c(1,j),a(b)) == 1</span>
+
-
<span class="comment">%            d(:,b+1) = c(:,j);</span>
+
-
<span class="comment">%        end</span>
+
-
<span class="comment">%    end</span>
+
-
<span class="comment">% end</span>
+
-
<span class="comment">% d</span>
+
-
</pre><pre class="codeoutput">
+
-
ans =
+
-
    '0'        '00'        '01'        '10'        '11'   
+
[2] [http://en.wikipedia.org/wiki/Goldbeter-Koshland_kinetics Goldbeter-Koshland kinetics In <i>Wikipedia.</i> Retrieved July 13, 2010, from http://en.wikipedia.org/wiki/Goldbeter-Koshland_kinetics]
-
    '000000'    '000000'    '010100'    '101000'    '111100'
+
</div>
-
    '000001'    '000000'    '010100'    '101000'    '111100'
+
-
    '000010'    '000000'    '010100'    '101000'    '111100'
+
-
    '000011'    '000000'    '010100'    '101000'    '111100'
+
-
    '000100'    '000000'    '010100'    '101000'    '111100'
+
-
    '000101'    '000000'    '010100'    '101000'    '111100'
+
-
    '000110'    '000000'    '010100'    '101000'    '111100'
+
-
    '000111'    '000000'    '010100'    '101000'    '111100'
+
-
    '001000'    '000000'    '010100'    '101000'    '111100'
+
-
    '001001'    '000000'    '010100'    '101000'    '111100'
+
-
    '001010'    '000000'    '010100'    '101000'    '111100'
+
-
    '001011'    '000000'    '010100'    '101000'    '111100'
+
-
    '001100'    '000000'    '010100'    '101000'    '111100'
+
-
    '001101'    '000000'    '010100'    '101000'    '111100'
+
-
    '001110'    '000000'    '010100'    '101000'    '111100'
+
-
    '001111'    '000000'    '010100'    '101000'    '111100'
+
-
    '010000'    '000001'    '010101'    '101001'    '111101'
+
-
    '010001'    '000001'    '010101'    '101001'    '111101'
+
-
    '010010'    '000001'    '010101'    '101001'    '111101'
+
-
    '010011'    '000001'    '010101'    '101001'    '111101'
+
-
    '010100'    '000001'    '010101'    '101001'    '111101'
+
-
    '010101'    '000001'    '010101'    '101001'    '111101'
+
-
    '010110'    '000001'    '010101'    '101001'    '111101'
+
-
    '010111'    '000001'    '010101'    '101001'    '111101'
+
-
    '011000'    '000001'    '010101'    '101001'    '111101'
+
-
    '011001'    '000001'    '010101'    '101001'    '111101'
+
-
    '011010'    '000001'    '010101'    '101001'    '111101'
+
-
    '011011'    '000001'    '010101'    '101001'    '111101'
+
-
    '011100'    '000001'    '010101'    '101001'    '111101'
+
-
    '011101'    '000001'    '010101'    '101001'    '111101'
+
-
    '011110'    '000001'    '010101'    '101001'    '111101'
+
-
    '011111'    '000001'    '010101'    '101001'    '111101'
+
-
    '100000'    '000010'    '010110'    '101010'    '111110'
+
-
    '100001'    '000010'    '010110'    '101010'    '111110'
+
-
    '100010'    '000010'    '010110'    '101010'    '111110'
+
-
    '100011'    '000010'    '010110'    '101010'    '111110'
+
-
    '100100'    '000010'    '010110'    '101010'    '111110'
+
-
    '100101'    '000010'    '010110'    '101010'    '111110'
+
-
    '100110'    '000010'    '010110'    '101010'    '111110'
+
-
    '100111'    '000010'    '010110'    '101010'    '111110'
+
-
    '101000'    '000010'    '010110'    '101010'    '111110'
+
-
    '101001'    '000010'    '010110'    '101010'    '111110'
+
-
    '101010'    '000010'    '010110'    '101010'    '111110'
+
-
    '101011'    '000010'    '010110'    '101010'    '111110'
+
-
    '101100'    '000010'    '010110'    '101010'    '111110'
+
-
    '101101'    '000010'    '010110'    '101010'    '111110'
+
-
    '101110'    '000010'    '010110'    '101010'    '111110'
+
-
    '101111'    '000010'    '010110'    '101010'    '111110'
+
-
    '110000'    '000000'    '010100'    '101000'    '111100'
+
-
    '110001'    '000000'    '010100'    '101000'    '111100'
+
-
    '110010'    '000000'    '010100'    '101000'    '111100'
+
-
    '110011'    '000000'    '010100'    '101000'    '111100'
+
-
    '110100'    '000000'    '010100'    '101000'    '111100'
+
-
    '110101'    '000000'    '010100'    '101000'    '111100'
+
-
    '110110'    '000000'    '010100'    '101000'    '111100'
+
-
    '110111'    '000000'    '010100'    '101000'    '111100'
+
-
    '111000'    '000000'    '010100'    '101000'    '111100'
+
-
    '111001'    '000000'    '010100'    '101000'    '111100'
+
-
    '111010'    '000000'    '010100'    '101000'    '111100'
+
-
    '111011'    '000000'    '010100'    '101000'    '111100'
+
-
    '111100'    '000000'    '010100'    '101000'    '111100'
+
-
    '111101'    '000000'    '010100'    '101000'    '111100'
+
-
    '111110'    '000000'    '010100'    '101000'    '111100'
+
-
    '111111'    '000000'    '010100'    '101000'    '111100'
+
-
 
+
[3] [http://www.ncbi.nlm.nih.gov/pubmed/18938177 Buchler NE, Luis M. Molecular titration and ultrasensitivity in regulatory networks. J. Mol. Biol. 2008 Dec 31; 384(5):1106-19]
-
SS_mXn_Input =
+
-
 
+
-
    '000000'    '1  1'      '00'
+
-
    '010101'    '22  2'    '01'
+
-
    '101010'    '43  3'    '10'
+
-
    '111100'    '61  4'    '11'
+
-
 
+
-
</pre><p class="footer"><br>
+
-
      Published with MATLAB&reg; 7.10<br></p></div><!--
+
-
##### SOURCE BEGIN #####
+
-
clear all
+
-
clc
+
-
 
+
-
%Constants and Values
+
-
trackingNum = 6;    %mRNA_pA, mRNA_pB, sRNA_A, sRNA_B, protein_A, protein_B;
+
-
inputNum = 2;      %A, B;
+
-
processNum = 6;    %Trx_pA, Trx_sRNA_A, Trx_pB, Trx_sRNA_B, Trl_A, Trl_B;
+
-
 
+
-
%Cell/Matrix Dimensions
+
-
m = 2^trackingNum;
+
-
n = 2^inputNum;
+
-
c = cell(m+1, n+1);
+
-
 
+
-
trackingMatrix = de2bi(0:m-1);
+
-
inputMatrix = de2bi(0:n-1);
+
-
processMatrix = zeros(1,processNum);
+
-
 
+
-
%Populating the Cell (Tracking x Input)
+
-
c{1,1} = [0];
+
-
for j = 1
+
-
    for i = 2:m+1
+
-
        c{i,j} = trackingMatrix(i-1,:);
+
-
    end
+
-
end
+
-
for i = 1
+
-
    for j = 2:n+1
+
-
        c{i,j} = inputMatrix(j-1,:);
+
-
    end
+
-
end
+
-
for i = 2:m+1
+
-
    for j = 2:n+1
+
-
        c{i,j} = processMatrix;
+
-
    end
+
-
end
+
-
 
+
-
%Rules, Acessing, and Changing
+
-
for j = 2:n+1
+
-
    A = c{1,j}(1);
+
-
    B = c{1,j}(2);
+
-
   
+
-
    for i = 2:m+1
+
-
        mRNA_pA = c{i,1}(1);
+
-
        mRNA_pB = c{i,1}(2);
+
-
        sRNA_A = c{i,1}(3);
+
-
        sRNA_B = c{i,1}(4);
+
-
        protein_A = c{i,1}(5);
+
-
        protein_B = c{i,1}(6);
+
-
       
+
-
        %Trx_pA
+
-
        if A == 1
+
-
            c{i,j}(1) = 1;
+
-
        end
+
-
       
+
-
        %Trx_pB
+
-
        if B == 1
+
-
            c{i,j}(2) = 1;
+
-
        end
+
-
       
+
-
        %Trx_sRNA_A
+
-
        if A == 1
+
-
            c{i,j}(3) = 1;
+
-
        end
+
-
       
+
-
        %Trx_sRNA_B
+
-
        if B == 1
+
-
            c{i,j}(4) = 1;
+
-
        end
+
-
       
+
-
        %Trl_A
+
-
        if mRNA_pA == 1 && mRNA_pB == 0
+
-
            c{i,j}(5) = 1;
+
-
        end
+
-
       
+
-
        %Trl_B
+
-
        if mRNA_pB == 1 && mRNA_pA == 0
+
-
            c{i,j}(6) = 1;
+
-
        end
+
-
       
+
-
    end
+
-
end
+
-
 
+
-
%Display Results (Column by Column)
+
-
[nrows,ncols]= size(c);
+
-
%Condense Cell and Display
+
-
for i = 1:nrows
+
-
    for j = 1:ncols       
+
-
        string = num2str(c{i,j});
+
-
        l = length(string);
+
-
        r = 1;
+
-
        s = 1;
+
-
        t = 0;
+
-
       
+
-
        while t ~= 1
+
-
            if r == l
+
-
            t = 1;
+
-
            end
+
-
           
+
-
            noSpacesString(s) = string(r);
+
-
            r = r+3;
+
-
            s = s+1;
+
-
        end
+
-
        c{i,j} = noSpacesString;
+
-
    end
+
-
end
+
-
c(:,:)
+
-
 
+
-
%Find Steady States and Corresponding Inputs
+
-
counter = 1;
+
-
for i = 2:m+1
+
-
    for j = 2:n+1
+
-
        if c{i,j} == c{i,1}
+
-
            completeMatrix{counter,1} = c{i,j};            %Steady state values
+
-
            completeMatrix{counter,2} = num2str([i-1,j-1]); %Location (n x m) within results area
+
-
            completeMatrix{counter,3} = c{1,j};            %Corresponding input values           
+
-
            counter = counter+1;
+
-
        end
+
-
    end
+
-
end
+
-
SS_mXn_Input = completeMatrix
+
-
 
+
-
time = 0:processNum;
+
-
%plot(time,,time,,time,,time,,time,,time,)
+
-
 
+
-
%New Cell for Specific Cases
+
-
% d(:,1) = c(:,1);
+
-
% for j = 2:n+1
+
-
%    C1 = '0000';
+
-
%    C2 = '0011';
+
-
%    C3 = '0100';
+
-
%    C4 = '0111';
+
-
%    C5 = '1000';
+
-
%    C6 = '1011';
+
-
%    C7 = '1100';
+
-
%   
+
-
%    a = {C1, C2, C3, C4, C5, C6, C7};
+
-
%    for b = 1:1:length(a)
+
-
%        if strcmp(c(1,j),a(b)) == 1
+
-
%            d(:,b+1) = c(:,j);
+
-
%        end
+
-
%    end
+
-
% end
+
-
% d
+
-
##### SOURCE END #####
+
-
--></body>
+
-
</html>
+
-
 
+
-
 
+
-
==Kinase/Phosphatase System==
+
-
[[Image:MainGBK.JPG]]
+
-
 
+
-
From Michaelis-Menten kinetics we know that the rate at which Zp is dephosphorylated is [[Image:R1.JPG]]
+
-
and the rate at which Z is phosphorylated is
+
-
[[Image:R2.JPG]]
+
-
 
+
-
Along with the conservation equation [Z]o = [Zp] + [Z],
+
-
[[Image:1stblock.jpg]]
+
-
Where
+
-
[[Image:2ndblock.jpg]]
+
-
[[Image:3rdblock.jpg]]
+
-
Now, assume that the two opposing enzymes are nowhere near being saturated with substrate:
+
-
[[Image:4thblock.jpg]]
+
-
So, the fraction of modified substrate is a saturating function of the ratio of inputs. The half-max value is the ratio of the strengths of the two enzymes.   The linear regime of this function exists where
+
-
[[Image:5thblock.jpg]]
+
-
And the fraction of unmodified substrate is a linear function of the ratio of inputs:
+
-
[[Image:6thblock.jpg]]
+
-
So, the requirements for this analog ratio sensor are
+
-
1. Consistent relationships between inputs and enzyme activities (non-trivial)
+
-
2. A non-saturating amount of substrate
+
-
3. A ratio of enzyme activities greater than any ratios we want to measure
+
-
Now increase the amount of substrate to saturation and
+
-
[[Image:7thblock.jpg]]
+
-
[[Image:8thblock.jpg]]
+
-
modified.  Any ratio above and all the substrate becomes unmodified.  The requirements for this digital ratio sensor are:
+
-
1. Consistent relationships between inputs and enzyme activities (non-trivial)
+
-
2. An amount of substrate sufficient to saturate both opposing enzymes
+
-
 
+
-
 
+
-
 
+
-
</div>
+

Latest revision as of 03:56, 28 October 2010

Home Project Applications Modeling Parts Team Notebook Twitter

Contents

Goals

Our intuition for what makes a good ratio sensor could only take us so far. From the very first stages of design, we wanted to back up and test our ideas with mathematical tools. Luckily, we found that solving the equations of mass action kinetics at steady-state was enough to give us clear design criteria. We present the mathematical basis for sensors that are capable of sensing a single ratio digitally, or many ratios in an analog fashion.

Kinase/Phosphatase System

Throughout this derivation, we refer to Goldbeter and Koshland's seminal work on the kinetics of emzyme pairs [1]. For an opposing pair of enzymes X and Y modifying and unmodifying a substrate Z with modification p,

MainGBK.JPG

From Michaelis-Menten kinetics we know that the rate at which Zp is dephosphorylated is

R1.JPG [2]

and the rate at which Z is phosphorylated is

R2.JPG [2]

We also know that Z can be modified an unmodified, but its total is conserved: [Z]o = [Zp] + [Z]

At steady state, modification and unmodification rates are equal, leading us to

1stblock.JPG [2]

where

2nd block.JPG [2]


Rearranging gives

3rdblock.JPG

Now, assume that the two opposing enzymes are nowhere near being saturated with substrate:

4thblock.JPG

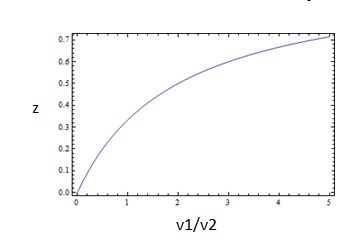
which is the equation for a Michaelis-Menten-shaped curve as shown below:

Langmuir.JPG

So, the fraction of modified substrate is a saturating function of the ratio of inputs, the half-max value is the ratio of the strengths of the two enzymes, and the fraction of unmodified substrate is a linear function of the ratio of inputs,

6thblock.JPG

We now know that the requirements for this analog ratio sensor are

  1. Consistent relationships between inputs and enzyme activities (non-trivial)
  2. A non-saturating amount of substrate

But what happens if we disobey requirement 1? Let's increase the amount of substrate to saturation so that

7thblock.JPG
8thblock.JPG

When the enzymes are saturated, the only steady-state solution is v1 = v2. Any ratio of v1/v2 below this, and all the substrate becomes modified. Any ratio above and all the substrate becomes unmodified. Simply by changing the concentration of substrate, we have converted our analog ratio sensor to a digital ratio sensor.

The requirements for this digital ratio sensor are:

  1. Consistent relationships between inputs and enzyme activities (non-trivial)
  2. An amount of substrate sufficient to saturate both opposing enzymes

sRNA System

This sRNA system is bases its analysis on the work of Nicolas Buchler. [3]

Consider an sRNA that can bind to an mRNA and inhibit its translation. The pair binds and dissociates with dissociation constant Kd.

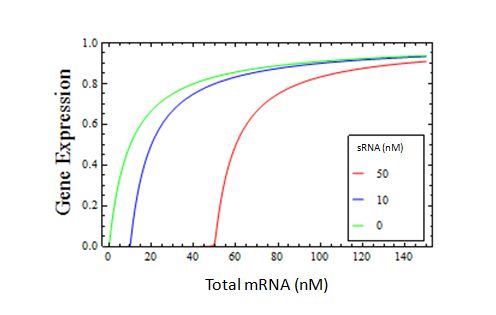
For a moment, imagine that this interaction is infinitely strong, such that Kd -> 0. In this case, all the mRNA available will bind to the sRNA, until every sRNA is occupied by one mRNA. Once this threshold, defined by the total sRNA concentration, is reached, additional mRNA added is free to be translated. Here we show the accumulation of translatable free mRNA, and hence Gene Expression vs. total mRNA, in the presence of varying concentrations of infinitely strong sRNA

SRNA1.JPG

At the point that the sRNA becomes saturated, two interesting things occur.

  1. There is a sharp transition between no gene expression and a linearly-increasing amount of gene expression.
  2. This transition occurs only when the concentration of mRNA is equal to the concentration of sRNA.

We have designed a sensor that responds to a 1:1 mRNA:sRNA ratio with a sharp change in output.

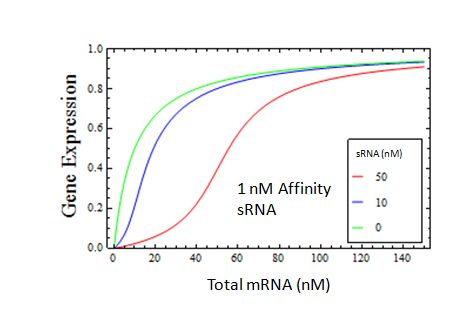
But will this system have the same desirable properties when the sRNA is only realistically strong? Here we assume a 1 nM interaction between sRNA and mRNA

SRNA2.JPG

We find that the transition is still quite sharp when the sRNA has a realistic dissociation constant.

References

[1] [http://www.ncbi.nlm.nih.gov/pubmed/6947258 Goldbeter A, Koshland DE Jr.: An amplified sensitivity arising from covalent modification in biological systems. PNAS. 1981 Nov; 78(11) 6840-4.]

[2] [http://en.wikipedia.org/wiki/Goldbeter-Koshland_kinetics Goldbeter-Koshland kinetics In Wikipedia. Retrieved July 13, 2010, from http://en.wikipedia.org/wiki/Goldbeter-Koshland_kinetics]

[3] [http://www.ncbi.nlm.nih.gov/pubmed/18938177 Buchler NE, Luis M. Molecular titration and ultrasensitivity in regulatory networks. J. Mol. Biol. 2008 Dec 31; 384(5):1106-19]
Retrieved from "http://2010.igem.org/Team:Stanford/Research/Modeling"