Team:Cambridge/Tools/Lighting
From 2010.igem.org
(→Modelling) |
|||
| (14 intermediate revisions not shown) | |||
| Line 24: | Line 24: | ||
=Modelling= | =Modelling= | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
To show that it may one day indeed be possible to have bioluminescent trees replacing street lamps we considered how efficicient the plants would have to be in order to match a low-intensity street lamp. | To show that it may one day indeed be possible to have bioluminescent trees replacing street lamps we considered how efficicient the plants would have to be in order to match a low-intensity street lamp. | ||
==Radiation In== | ==Radiation In== | ||
| - | + | {{:Team:Cambridge/Templates/RightImage|image=Solar_Spectrum.png|caption=''Figure 1: The solar radiation spectrum for direct light at both the top of the Earth's atmosphere and at sea level.''}} | |
Figure 1 shows the radiation spectrum recieved from the sun at sea level. In total this gives about '''1,321 – 1,471 W/m<sup>2</sup>''' of radiant energy for regions in North America. (Data supplied by American Society for Testing and Materials ([http://www.wmo.int/pages/prog/www/IMOP/publications/CIMO-Guide/CIMO%20Guide%207th%20Edition,%202008/Part%20I/Chapter%208.pdf. ASTM]) Terrestrial Reference Spectra, a common standard used in photovoltaics). | Figure 1 shows the radiation spectrum recieved from the sun at sea level. In total this gives about '''1,321 – 1,471 W/m<sup>2</sup>''' of radiant energy for regions in North America. (Data supplied by American Society for Testing and Materials ([http://www.wmo.int/pages/prog/www/IMOP/publications/CIMO-Guide/CIMO%20Guide%207th%20Edition,%202008/Part%20I/Chapter%208.pdf. ASTM]) Terrestrial Reference Spectra, a common standard used in photovoltaics). | ||
| Line 78: | Line 51: | ||
<tr> | <tr> | ||
<td><b>Light Source</b> | <td><b>Light Source</b> | ||
| - | |||
</td><td><b>Output(lumens)</b> | </td><td><b>Output(lumens)</b> | ||
</td></tr> | </td></tr> | ||
<tr> | <tr> | ||
<td>Incandescent | <td>Incandescent | ||
| - | |||
</td><td>210-2700 | </td><td>210-2700 | ||
</td></tr> | </td></tr> | ||
<tr> | <tr> | ||
<td>Fluorescent | <td>Fluorescent | ||
| - | |||
</td><td>1000-7500 | </td><td>1000-7500 | ||
</td></tr> | </td></tr> | ||
<tr> | <tr> | ||
<td>Metal Halide | <td>Metal Halide | ||
| - | |||
</td><td>1900-30000 | </td><td>1900-30000 | ||
</td></tr> | </td></tr> | ||
<tr> | <tr> | ||
<td>High-Pressure Sodium | <td>High-Pressure Sodium | ||
| - | |||
</td><td>3600-46000 | </td><td>3600-46000 | ||
</td></tr> | </td></tr> | ||
<tr> | <tr> | ||
<td>Low-Pressure Sodium | <td>Low-Pressure Sodium | ||
| - | |||
</td><td>1800-33000 | </td><td>1800-33000 | ||
</td></tr> | </td></tr> | ||
| Line 118: | Line 85: | ||
*'''Luminance''', which is measured in candelas per square metre (cd m<sup>-2</sup>). | *'''Luminance''', which is measured in candelas per square metre (cd m<sup>-2</sup>). | ||
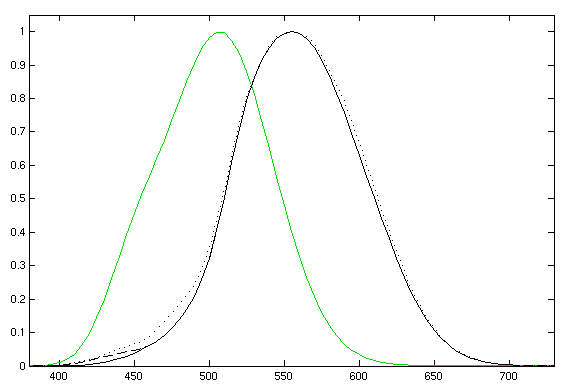
| - | If you look at a black object and ask "how much light is coming out of that?" there are two answers. The first is obviously none, since it appears black, but the second relies on the fact that it is possible that the object is very hot and is emitting in the infra-red, or is a source of UV and is thus emitting a lot of light. The two measures above quantify this difference. Radiance measures the actual electromagnetic radiation coming from an object, whereas luminance adjusts for the perceptive abilities of the human eye. If you look at figure | + | {{:Team:Cambridge/Templates/RightImage|image=photopicscotopic.png|caption=''Figure 2: Photopic (black) and scotopic (green) luminosity functions.''}} |
| + | |||
| + | If you look at a black object and ask "how much light is coming out of that?" there are two answers. The first is obviously none, since it appears black, but the second relies on the fact that it is possible that the object is very hot and is emitting in the infra-red, or is a source of UV and is thus emitting a lot of light. The two measures above quantify this difference. Radiance measures the actual electromagnetic radiation coming from an object, whereas luminance adjusts for the perceptive abilities of the human eye. If you look at figure 2 you can see the '''luminosity functions''' which supply this weighting in the visible part of the spectrum. | ||
There are two curves, one for photopic vision, and the latter for scotopic. The former is normal vision in good light and covers the normal range of colours. The latter is for dark vision, when the (colour percieving) cone cells are unable to function. This part of the reason why you can only see in black and white in the dark. | There are two curves, one for photopic vision, and the latter for scotopic. The former is normal vision in good light and covers the normal range of colours. The latter is for dark vision, when the (colour percieving) cone cells are unable to function. This part of the reason why you can only see in black and white in the dark. | ||
| + | |||
| + | {{:Team:Cambridge/Templates/RightImage|image=Luminosityfunction.png|caption=''Figure 3: The formula for calculating luminance. (F:Luminous Flux, y:Luminosity Function,J:Spectral Power Distribution,λ:Wavelength''}} | ||
To convert from Radiance to Luminance you integrate the power spectrum weighted by the luminosity function so that wavelengths beyond that of human perception are cut out. Note that this transformation is therefore one-way. You can't convert from Luminance to Radiance. | To convert from Radiance to Luminance you integrate the power spectrum weighted by the luminosity function so that wavelengths beyond that of human perception are cut out. Note that this transformation is therefore one-way. You can't convert from Luminance to Radiance. | ||
| Line 126: | Line 97: | ||
The measurements of light output taken above are in '''lumens''' (a measurement of Luminance) where 1lm=1cd*sr. The lumen thus quantifies the human-percieved total amount of light being emitted from an object. The above values use the scotopic luminosity function, since street lights operate in low-light conditions. | The measurements of light output taken above are in '''lumens''' (a measurement of Luminance) where 1lm=1cd*sr. The lumen thus quantifies the human-percieved total amount of light being emitted from an object. The above values use the scotopic luminosity function, since street lights operate in low-light conditions. | ||
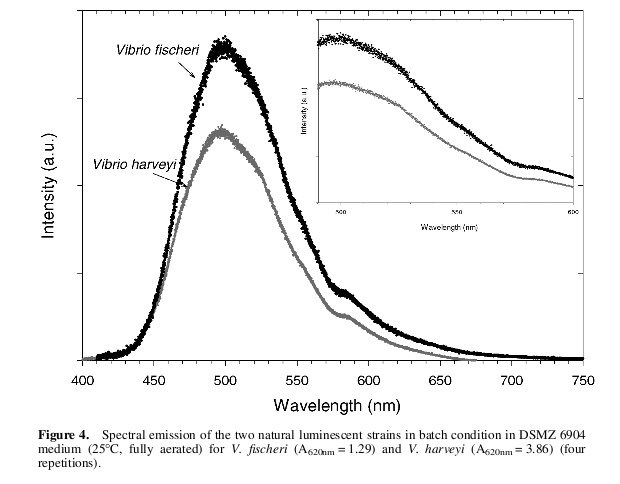
| - | We wrote a [[Team:Cambridge/luminanceSourceCode | | + | {{:Team:Cambridge/Templates/RightImage|image=Fischerispectrum.jpg|caption=''Figure 4: The emission spectrum of V. Fischeri (shown in black)''}} |
| + | |||
| + | We wrote a program ([[Team:Cambridge/luminanceSourceCode | source code]]) in c++ which allowed the user to input their own power spectrum and be told the resulting luminance measure. By inputting the curve shown in figure 4 which details the emission spectrum of the Vibrio Fischeri we found the formula: | ||
Total Bacterial Luminance(lm)=471.13 x Total Energy Output(W) | Total Bacterial Luminance(lm)=471.13 x Total Energy Output(W) | ||
| - | It should be noted that this is actually a really good conversion factor, only about 33% of the radiant energy is lost to the outer regions of human perception (at best 1lm = 683.002 W). This is due to the fact that (as you can see from the scotopic luminosity function in figure | + | It should be noted that this is actually a really good conversion factor, only about 33% of the radiant energy is lost to the outer regions of human perception (at best 1lm = 683.002 W). This is due to the fact that (as you can see from the scotopic luminosity function in figure 2) the human eye is better at seeing blue light in the dark than red light, and our bacterial light is clearly blue. |
==Bringing it all together== | ==Bringing it all together== | ||
| Line 136: | Line 109: | ||
Now we combined the above calculations. If we assume that the tree absorbs all light passing through its projected area '''A''' (not a bad approximation, since only a few percent is able to make it through the canopy) then the total radiant light energy falling on it during the day time per second is '''60*A''' W. If the total radiant energy outputted at night per second is '''E''', then the luminous flux is '''471.13E''' lm, which we desire to be as bright as a street lamp '''X''' lm, then combining these we find that the total efficiency of our plant has to be: | Now we combined the above calculations. If we assume that the tree absorbs all light passing through its projected area '''A''' (not a bad approximation, since only a few percent is able to make it through the canopy) then the total radiant light energy falling on it during the day time per second is '''60*A''' W. If the total radiant energy outputted at night per second is '''E''', then the luminous flux is '''471.13E''' lm, which we desire to be as bright as a street lamp '''X''' lm, then combining these we find that the total efficiency of our plant has to be: | ||
| - | Efficiency = (X*T<sub>night</sub>) / (471.13*60A*T<sub>day</sub>) | + | '''Efficiency = (X*T<sub>night</sub>) / (471.13*60A*T<sub>day</sub>)''' |
| - | where '''T<sub>day</sub>''' and '''T<sub>night</sub>''' are the hours of daylight and night time respectively. If we choose the least bright street lamp (X=210) and hypothesise a projected area of | + | where '''T<sub>day</sub>''' and '''T<sub>night</sub>''' are the hours of daylight and night time respectively. If we choose the least bright street lamp ('''X=210''') and hypothesise a projected area of '''A=30m<sup>2</sup>''', and a '''day:night ratio 14:10''' then we find that the efficiency must be roughly '''0.02%'''. This means that 0.02% of the total energy which the tree absorbs in photosynthesis must be converted eventually into light output, a potentially achievable target. |
{{:Team:Cambridge/Templates/footer}} | {{:Team:Cambridge/Templates/footer}} | ||
Latest revision as of 16:35, 27 October 2010

Bioluminescent street lamps
In order to provide any solution to the problem, a biological solution must tap into a currently unused energy resource. For this reason we decided to consider the use of bioluminescent trees to replace conventional street lamps.
A tree in this position would be able to photosynthesise during the day, building up reserves of energy. We then imagined it emitting light by night, using the bacterial luciferase system, under the control of the inherent circadian clock based gene regulation systems.
Putting it into practice
We wanted to provide some proof of concept of these ideas. We built the [http://www.youtube.com/watch?v=tUFscEVK5Ks bacterial bubble lamp] to investigate this, and also read the Jungle Book using a flask containing E. coli expressing our bacterial luciferase.
We had thought about bacteria being used for emergency lighting, and our advisor Fernan printed a fire exit sign, which was placed over a plate containing one of our strains of E. coli. In a real system we would imagine using anhydrobiosis to create bacteria 'in hibernation' which could be activated when needed.

Modelling
To show that it may one day indeed be possible to have bioluminescent trees replacing street lamps we considered how efficicient the plants would have to be in order to match a low-intensity street lamp.
Radiation In
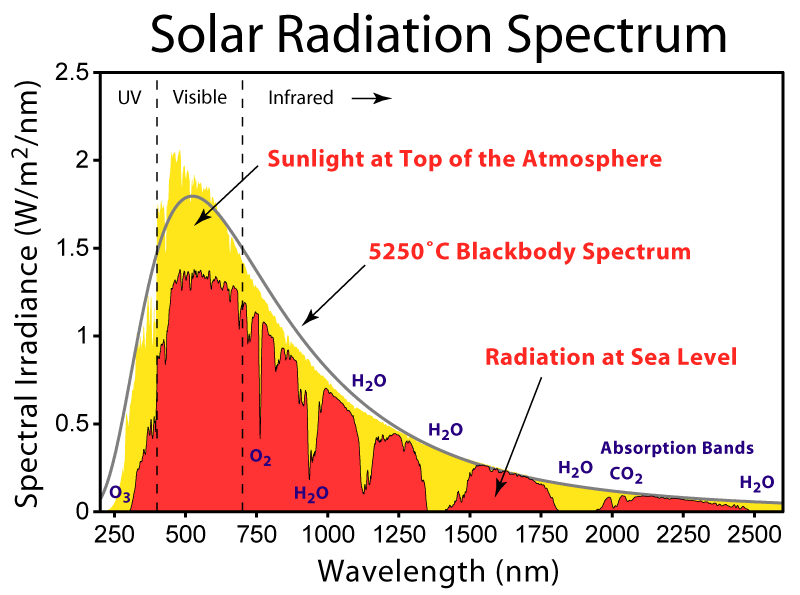
Figure 1 shows the radiation spectrum recieved from the sun at sea level. In total this gives about 1,321 – 1,471 W/m2 of radiant energy for regions in North America. (Data supplied by American Society for Testing and Materials ([http://www.wmo.int/pages/prog/www/IMOP/publications/CIMO-Guide/CIMO%20Guide%207th%20Edition,%202008/Part%20I/Chapter%208.pdf. ASTM]) Terrestrial Reference Spectra, a common standard used in photovoltaics).
This is a lot of energy, but of course most of it is not accessible to plants. They can only absorb in the visible region (corresponding to roughy 45% of total solar energy), radiation known as PAR (photosynthetically active radiation). In addition, there are other constraints, such as reflectivity of leaves and the absorption spectrum of chlorophyll. The net result is that in general plants are only able to take between 3 and 6% of total solar radiation, corresponding to roughly 60 W/m2 (Figures from Hall, D.O. and House, J.I., Biomass and Bioenergy, 6,11-30 (1994).)
Radiation out
Since that's the energy which plants have available to, we then considered what they need to be putting out in order to function as street lights.
| Light Source | Output(lumens) |
| Incandescent | 210-2700 |
| Fluorescent | 1000-7500 |
| Metal Halide | 1900-30000 |
| High-Pressure Sodium | 3600-46000 |
| Low-Pressure Sodium | 1800-33000 |
The above table shows the luminous flux, measured in lumens for several different types of light.
Lumens are a measure of luminous intensity. When it comes to "brightness" there are two distinct measurements;
- Radiance, which is measured in watts per square metre per steradian (W sr-1 m-2 and
- Luminance, which is measured in candelas per square metre (cd m-2).
If you look at a black object and ask "how much light is coming out of that?" there are two answers. The first is obviously none, since it appears black, but the second relies on the fact that it is possible that the object is very hot and is emitting in the infra-red, or is a source of UV and is thus emitting a lot of light. The two measures above quantify this difference. Radiance measures the actual electromagnetic radiation coming from an object, whereas luminance adjusts for the perceptive abilities of the human eye. If you look at figure 2 you can see the luminosity functions which supply this weighting in the visible part of the spectrum.
There are two curves, one for photopic vision, and the latter for scotopic. The former is normal vision in good light and covers the normal range of colours. The latter is for dark vision, when the (colour percieving) cone cells are unable to function. This part of the reason why you can only see in black and white in the dark.
To convert from Radiance to Luminance you integrate the power spectrum weighted by the luminosity function so that wavelengths beyond that of human perception are cut out. Note that this transformation is therefore one-way. You can't convert from Luminance to Radiance.
The measurements of light output taken above are in lumens (a measurement of Luminance) where 1lm=1cd*sr. The lumen thus quantifies the human-percieved total amount of light being emitted from an object. The above values use the scotopic luminosity function, since street lights operate in low-light conditions.
We wrote a program ( source code) in c++ which allowed the user to input their own power spectrum and be told the resulting luminance measure. By inputting the curve shown in figure 4 which details the emission spectrum of the Vibrio Fischeri we found the formula:
Total Bacterial Luminance(lm)=471.13 x Total Energy Output(W)
It should be noted that this is actually a really good conversion factor, only about 33% of the radiant energy is lost to the outer regions of human perception (at best 1lm = 683.002 W). This is due to the fact that (as you can see from the scotopic luminosity function in figure 2) the human eye is better at seeing blue light in the dark than red light, and our bacterial light is clearly blue.
Bringing it all together
Now we combined the above calculations. If we assume that the tree absorbs all light passing through its projected area A (not a bad approximation, since only a few percent is able to make it through the canopy) then the total radiant light energy falling on it during the day time per second is 60*A W. If the total radiant energy outputted at night per second is E, then the luminous flux is 471.13E lm, which we desire to be as bright as a street lamp X lm, then combining these we find that the total efficiency of our plant has to be:
Efficiency = (X*Tnight) / (471.13*60A*Tday)
where Tday and Tnight are the hours of daylight and night time respectively. If we choose the least bright street lamp (X=210) and hypothesise a projected area of A=30m2, and a day:night ratio 14:10 then we find that the efficiency must be roughly 0.02%. This means that 0.02% of the total energy which the tree absorbs in photosynthesis must be converted eventually into light output, a potentially achievable target.
 "
"