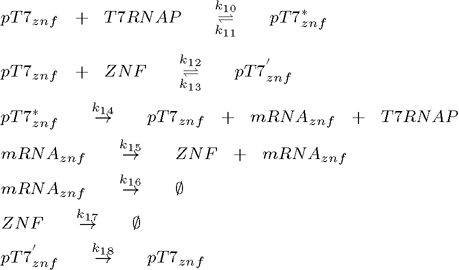Team:Slovenia/PROJECT/oscillator/smolen
From 2010.igem.org
| Line 56: | Line 56: | ||
As can be seen from the list of reactions, the model also includes degradation of all proteins, even when already bound to the DNA (Biham et al., 2007). It does not, however, consider repressor binding cooperativity, which was a component of all the existing genetic oscillators up to now, so the regulation of each gene is done by a monomeric protein (Hill coefficient equals 1). This is an important difference as many DNA binding proteins, such as ZNFs bind as monomers, while it has been argued that cooperativity is an essential feature of functional genetic oscillators as it ensures the nonlinearity (Biham et al, 2007). Nonlinearity is however, as we will show later, provided by the time delay which is a natural consequence of the subsequent transcription and translation step inherent in of all biological systems.<br><br> | As can be seen from the list of reactions, the model also includes degradation of all proteins, even when already bound to the DNA (Biham et al., 2007). It does not, however, consider repressor binding cooperativity, which was a component of all the existing genetic oscillators up to now, so the regulation of each gene is done by a monomeric protein (Hill coefficient equals 1). This is an important difference as many DNA binding proteins, such as ZNFs bind as monomers, while it has been argued that cooperativity is an essential feature of functional genetic oscillators as it ensures the nonlinearity (Biham et al, 2007). Nonlinearity is however, as we will show later, provided by the time delay which is a natural consequence of the subsequent transcription and translation step inherent in of all biological systems.<br><br> | ||
<br><br> | <br><br> | ||
| - | <h2> | + | <h2>Parameters and kinetics</h2> |
| + | |||
| + | Parameterss and kinetic rates used in the model were taken from several published models as we could not find one specific model that would provide all the necessary information. The degradation rate of mRNA was set to t1/2 = 2 min, and the degradation of proteins to t1/2 = 10 min (according to Elowitz et al., 2000). Processivity of the RNA polymerase was set to 200 nucleotides/second according to (McAllister, W. T., 1997), RNA polymerase initiation rate and dissociation rate used in the model were 50uM^-1 sec^-1 and 0.2 sec^-1 respectively (Kuzmine et al, 2002). Initiation and dissociation rate values of the typical published ZNF proteins were used (k_on = 0.031 uM^-1 sec^-1, k_off = 0.0002 sec^-1, Yang et al., 1995) and we plan to include the experimentally determined kinetic parameters of the ZNFs determined by SPR experiments.<br><br> | ||
| - | |||
| - | |||
The model is similar to one described by Stricker in "A fast, robust and tunable synthetic gene oscillator" (Stricker et al., 2008) although different building blocks were used (different repressors, promoter and RNA polymerase). Once the model was assembled, the right tool for modeling had to be found. As both deterministic and stochastic models were made, different tools were used for both, but results from the two types of simulations were comparable. | The model is similar to one described by Stricker in "A fast, robust and tunable synthetic gene oscillator" (Stricker et al., 2008) although different building blocks were used (different repressors, promoter and RNA polymerase). Once the model was assembled, the right tool for modeling had to be found. As both deterministic and stochastic models were made, different tools were used for both, but results from the two types of simulations were comparable. | ||
<hr /> | <hr /> | ||
| + | |||
Paul Smolen, Douglas A. Baxter and John H. Byrne, Department of Neurobiology and Anatomy, University of Texas, Medical School, Houston, Texas, 1998. Frequency selectivity, multistability, and oscillations emerge from models of genetic regulatory system. | Paul Smolen, Douglas A. Baxter and John H. Byrne, Department of Neurobiology and Anatomy, University of Texas, Medical School, Houston, Texas, 1998. Frequency selectivity, multistability, and oscillations emerge from models of genetic regulatory system. | ||
Am J Physiol Cell Physiol 274: 531-542. | Am J Physiol Cell Physiol 274: 531-542. | ||
Revision as of 19:55, 27 October 2010
Contents |
Smolen oscillator
The core of Smolen oscillator (Smolen et al., 1998) consists of two genes connected through double feedback loops. We have modified the design of the experimentally tested Smolen oscilator to include the orthogonal components as outlined in the selection of biological parts. Product of first gene is T7 RNA polymerase, which promotes transcription of both genes, while the product of the second gene is an artificial DNA-binding repressor (ZNF or TAL), which represses transcription of both genes. To observe the process described we also have a reporter gene coding for a Venus fluorescent protein under the control of the same and has no other function than reporting the current state of the oscillator. Its transcription is promoted by T7 RNA polymerase and repressed by the artificial DNA-binding repressor. Because we used the same promoter for all three constructs the kinetic complexity of the system was reduced significantly, since it allows us to use same parameters for different genes. To ensure the continuous oscillations and to avoid degeneration into the equilibrium state, we also included a gene under the constitutive promoter for the low continuous production of T7 RNA polymerase, which represents an important difference to the existing models of this type of genetic oscillator.

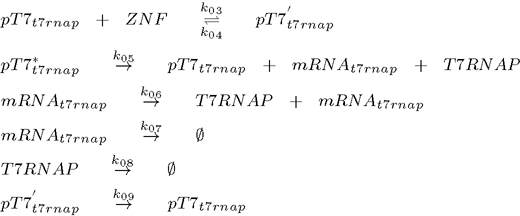
To model this system the following reactions were considered (pT7* is activated promoter, while pT7' is repressed promoter):
1. plasmid (T7 RNA polymerase under the control of T7 promoter):
2. plasmid (transcriptional repressor ZNF under the control of T7 promoter):
3. plasmid (yellow fluorescent protein Venus under the control of T7 promoter):
4. plasmid (T7 RNA polymerase under the control of constitutive cytomegalovirus promoter):
In eukaryotic cells these four plasmids were used, however in prokaryotic cells the first three genes can be assembled into one plasmid, while T7 RNAP is provided from the integrated DE3 transposon as in E. coli BL21(DE3).
As can be seen from the list of reactions, the model also includes degradation of all proteins, even when already bound to the DNA (Biham et al., 2007). It does not, however, consider repressor binding cooperativity, which was a component of all the existing genetic oscillators up to now, so the regulation of each gene is done by a monomeric protein (Hill coefficient equals 1). This is an important difference as many DNA binding proteins, such as ZNFs bind as monomers, while it has been argued that cooperativity is an essential feature of functional genetic oscillators as it ensures the nonlinearity (Biham et al, 2007). Nonlinearity is however, as we will show later, provided by the time delay which is a natural consequence of the subsequent transcription and translation step inherent in of all biological systems.
Parameters and kinetics
Parameterss and kinetic rates used in the model were taken from several published models as we could not find one specific model that would provide all the necessary information. The degradation rate of mRNA was set to t1/2 = 2 min, and the degradation of proteins to t1/2 = 10 min (according to Elowitz et al., 2000). Processivity of the RNA polymerase was set to 200 nucleotides/second according to (McAllister, W. T., 1997), RNA polymerase initiation rate and dissociation rate used in the model were 50uM^-1 sec^-1 and 0.2 sec^-1 respectively (Kuzmine et al, 2002). Initiation and dissociation rate values of the typical published ZNF proteins were used (k_on = 0.031 uM^-1 sec^-1, k_off = 0.0002 sec^-1, Yang et al., 1995) and we plan to include the experimentally determined kinetic parameters of the ZNFs determined by SPR experiments.
The model is similar to one described by Stricker in "A fast, robust and tunable synthetic gene oscillator" (Stricker et al., 2008) although different building blocks were used (different repressors, promoter and RNA polymerase). Once the model was assembled, the right tool for modeling had to be found. As both deterministic and stochastic models were made, different tools were used for both, but results from the two types of simulations were comparable.
Paul Smolen, Douglas A. Baxter and John H. Byrne, Department of Neurobiology and Anatomy, University of Texas, Medical School, Houston, Texas, 1998. Frequency selectivity, multistability, and oscillations emerge from models of genetic regulatory system.
Am J Physiol Cell Physiol 274: 531-542.
Ofer Biham, Adiel Loinger, Racah Institute of Physics, Jerusalem, Israel, 2007. Stochastic simulations of the repressilator circuit.
PHYSICAL REVIEW E 76, 051917: 1-9
Michael B. Elowitz, Stanislas Leibler, Departments of Molecular Biology and Physics, Princeton University, USA, 2000. A synthetic oscillatory network of transcriptional regulators.
Nature Vol 403: 335-338
McAllister, W. T., 1997. Transcription by T7 RNA polymerase.
Nucleic Acids Mol. Biol. 11: 15–25
Iaroslav Kuzmine, Craig T Martin, 2002. Pre-steady-state kinetics of initiation of transcription by T7 RNA polymerase: a new kinetic model.
J. Mol. Biol. 305: 559-566
Wei-Ping Yang, Herren Wu, Carlos F Barbas III, 1995. Surface plasmon resonance based kinetic studies of zinc finger-DNA interactions.
Journal of Immunological Methods, 183: 175-182
 "
"