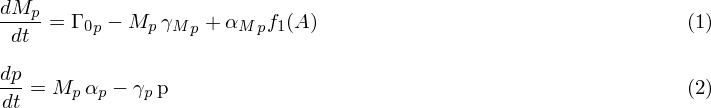Team:Stockholm/Modelling/Final eq
From 2010.igem.org
(Difference between revisions)
(New page: {{Stockholm/modelling}} ==== Yildirim N et al model ==== In a series of 5 equations, They proposed dynamics for mRNA production, <VAR>β</VAR>-galactosidase production, Allolactose...) |
|||
| (16 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{Stockholm/modelling}} | {{Stockholm/modelling}} | ||
| + | {| | ||
| + | |[[image:SU_modelling_Icon.gif|200px]] | ||
| + | |width="10px"| | ||
| + | |width="590px" align="justify"| | ||
| + | === A new gene and protein? === | ||
| - | + | After having the gene expressed in ''E. Coli'' the model that we came up with after studying extensively the articles [1]-[7] is as eq. 1 and eq. 2; where eq. 1 represents the dynamics for mRNA and eq. 2 represents the dynamics of protein translated from mRNA. These two equations are not complete though. | |
| + | [[image:SU_final_equation.png|580px]] | ||
| - | |||
| - | |||
| + | In these equations there are variables that need to be defined and values found. The description to how to find the values are as below: | ||
| - | This | + | *<VAR>Γ<sub>0</sub></VAR>: This spontaneous rate of mRNA production through translation. This variable can be *:calculated from Bremer H. et al. 1996 (mRNA elongation rate). In this case this means that sometimes ''lacI'' *:unbinds and lets the RNAP to bind and start translation. However RNAP binding strength needed to be discussed, which *:we will talk more about on discussion |
| + | *<VAR>γ<sub>M<sub>P</sub></sub></VAR> and <VAR>α<sub>M<sub>P</sub></sub></VAR>: for this case our approach is same as Yildirim et. al. 2003. We solve a system of equations for A = 0 and A <VAR>→∞</VAR>, in which when A = 0 we have no induction, and A <VAR>→∞</VAR> means high induction. At A <VAR>→∞</VAR>, we can assume that ,depending on the bacteria growth factor, mRNA production is increased at least 500folds (This is very dependent on the number of plasmids inside bacteria, environment and growth factor). So from these information one can calculate <VAR>γ<sub>M<sub>P</sub></sub></VAR> and <VAR>α<sub>M<sub>P</sub></sub></VAR>. | ||
| + | *<VAR>γ<sub>P</sub></VAR> and <VAR>α<sub>P</sub></VAR>: Unfortunately we couldn't find a reliable source for making scientific guess about degradation and production rate. However, one can from put forward reasonable values for these variables based on number of active ribosomes, growth factor, environment and translation elongation rate. These can be found in Bremer H. et al 1996. | ||
| - | + | So as a final model, we propose equations 1 and 2, and equations 7.1 to 7.4e from "Proposing the model" section as the toy model for protein production prediction for our genes. | |
| - | + | |} | |
| - | + | ||
| + | {{Stockholm/Footer}} | ||
Latest revision as of 19:42, 27 October 2010
 |

|
 |

|
 |

|

|

|
 "
"