Team:ETHZ Basel/Modeling/Movement
From 2010.igem.org
(→Modeling of the bacterial movement) |
|||
| Line 3: | Line 3: | ||
= Modeling of the bacterial movement = | = Modeling of the bacterial movement = | ||
| - | |||
| - | |||
[[Image:ETHZ_Basel_molecular_move.png|thumb|400px|'''Schematical overview of the relation between chemotaxis and the movement model.''']] | [[Image:ETHZ_Basel_molecular_move.png|thumb|400px|'''Schematical overview of the relation between chemotaxis and the movement model.''']] | ||
| + | Analogous to the highly complex signal transduction in the Chemotaxis receptor model, there is an equally challenging molecular system on side of the flagella, responsible for the movement of the bacterium. | ||
| + | In analyzing this system, we implemented a probabilistic model, meant to realistically simulate the behavior of the cell, by reproducing the main statistical features of the existing empirical data [1]. | ||
| + | The chemotactic movement might employ two states, either running or tumbling. The factor influencing the outcome of the flagellar system is CheYp concentration received as an input from the [https://2010.igem.org/Team:ETHZ_Basel/Modeling/Chemotaxis Chemotaxis pathway] at every time point of the simulation. | ||
| + | The link between CheYp concentration and the type of movement chosen by the bacterium is called '''bias''' and it is formally defined as the fraction of time spent in the running state with respect to the total observation time. Our choice for bias formulation is a non - linear Hill - type function of the CheYp concentration, with one of the parameters being the CheYp concentration for which a steady - state bias was obtained '''[NEED FURTHER EXPLANATION!!!]''' | ||
| - | |||
| - | |||
| + | |||
| + | From the already - known CheYp - CCW movement dependency (or bias), the probability of CCW movement (running) for the given CheYp concentration and for the given time - point is obtained. The cell then probabilistically chooses whether to run or to tumble. The choice of the running state is equivalent to a change in spatial coordinates, together with a slight change in direction (movement angle), while the choice of the tumbling state corresponds to new movement angle and unchanged spatial coordinates. During tumbling, the angle change was sampled from a normal distribution, with mean and variance obtained from the literature. [1] | ||
| + | |||
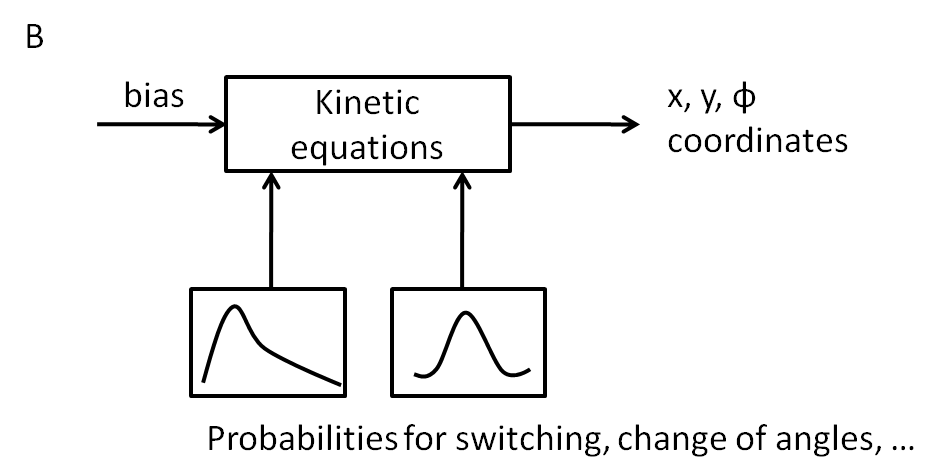
| + | [[Image:B1.png|center|600px|Sketch for a possible implementation of the controller.]] | ||
The biggest challenge regarding the movement model was obtaining a time - step - invariant behavior of the cell, whose reliability of statistical estimates should be the same, regardless of how often the cell had to choose its future state. | The biggest challenge regarding the movement model was obtaining a time - step - invariant behavior of the cell, whose reliability of statistical estimates should be the same, regardless of how often the cell had to choose its future state. | ||
Revision as of 11:05, 18 October 2010
Modeling of the bacterial movement
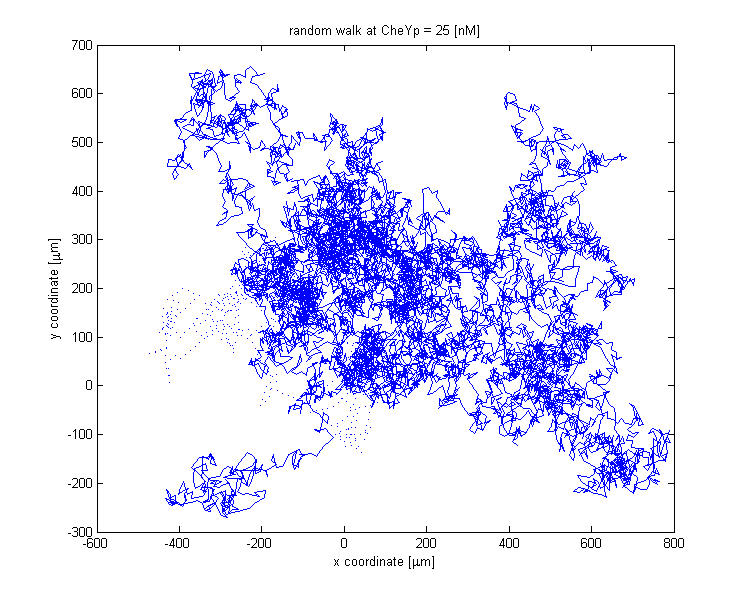
Analogous to the highly complex signal transduction in the Chemotaxis receptor model, there is an equally challenging molecular system on side of the flagella, responsible for the movement of the bacterium. In analyzing this system, we implemented a probabilistic model, meant to realistically simulate the behavior of the cell, by reproducing the main statistical features of the existing empirical data [1]. The chemotactic movement might employ two states, either running or tumbling. The factor influencing the outcome of the flagellar system is CheYp concentration received as an input from the Chemotaxis pathway at every time point of the simulation. The link between CheYp concentration and the type of movement chosen by the bacterium is called bias and it is formally defined as the fraction of time spent in the running state with respect to the total observation time. Our choice for bias formulation is a non - linear Hill - type function of the CheYp concentration, with one of the parameters being the CheYp concentration for which a steady - state bias was obtained [NEED FURTHER EXPLANATION!!!]
From the already - known CheYp - CCW movement dependency (or bias), the probability of CCW movement (running) for the given CheYp concentration and for the given time - point is obtained. The cell then probabilistically chooses whether to run or to tumble. The choice of the running state is equivalent to a change in spatial coordinates, together with a slight change in direction (movement angle), while the choice of the tumbling state corresponds to new movement angle and unchanged spatial coordinates. During tumbling, the angle change was sampled from a normal distribution, with mean and variance obtained from the literature. [1]
The biggest challenge regarding the movement model was obtaining a time - step - invariant behavior of the cell, whose reliability of statistical estimates should be the same, regardless of how often the cell had to choose its future state. In order to achieve this, we opted for a two - state model, in which the probability of running was controlled separately depending on whether the cell was running or tumbling.
The main assumption of our model was that the mean time in tumbling (mean tumbling length) is constant, while the mean time in running (mean running length) is a function of the bias. This assumption was made in accordance with existent published empirical data analyzing the chemotaxis movement. [citation]
The movement velocity was also considered constant [citation]
We derived the two central parameters of our model - the running probabilities - by exploiting the mathematical dependency between the mean run/tumbling length and the running/tumbling probabilities:
[derivation of the probability formulas]
!PENDING!
A first implementation was performed by linking the CheYp concentration to the probability of being in the run or tumbling state. These two states either describe the movement and the reorientation as difference equations that can be evaluated at discrete time points. Based on literature statistics about the distribution of change in angle due to tumbling a weibull distribution was selected:
[1] Chemotaxis in Escherichia coli analysed by three - dimensional Tracking. H.C. Berg, D.A.Brown: Nature 239, 500 - 504. 1972
 "
"