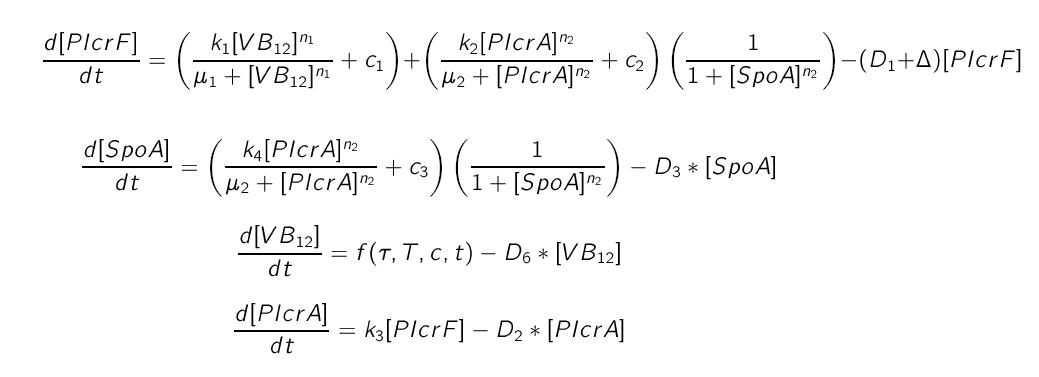Team:WITS-South Africa/Modelling
From 2010.igem.org

Contents |
Introduction
The biological sciences have generally been qualitative fields of study. However, due to the "top up" approach of synthetic biology, the need for quantitative mathematical models naturally arises. These models allow the biological system to be simulated and are necessary if control of the system is desired. We attempt to model a genetically engineered system implemented in the bacterium lactobacilus gasserii that is capable of detecting the presence of a pathogen, expressing a reported and also signaling others cells of the presence of the pathogen.
Project Outline
The aim of our machine is to identify an infection of Human papillomavirus in vivo. From a modelling point of view the mechanism has a number of points of interest expounded on in the following sections.
Extracellular Activity: Varying concentrations and effects of the genetic machine on the habitat outside the cell
Intracellular Activity: Responses to inputs and outputs as well as feedback loops
Intercellular Activity: A medium for communication between cells
Modelling
The benefits of modelling reach far beyond a theoretical understanding of a system. Models allow us to determine how we hope a system will behave. From this and experimental findings we can go on to determine where assumptions and simplifications made are critically important, whether it be positively or negatively.
Components of the Model
Extracellular Model
The extracellular model describes the change in substances outside of the cell. These fluctuations are modeled by a system of differential equations, which are likely to be non linear and of an order higher than one. This model will be used to try and describe each cell as a 'black box'. This will then be used to model the intercellular communication.
Intercellular Model (Cell Communication)
This portion of the model describes the behaviour of the cells as a network of communicating individuals. They communicate via a signalling process called quorum sensing.
Intracellular Model (Genetic Circuit)
The genetic circuit describes the biochemical reactions taking place inside the cell. The intracellular model describes the fluctuations in concentrations of each substance by modelling each chemical reaction by means of an appropriate kinetic law.
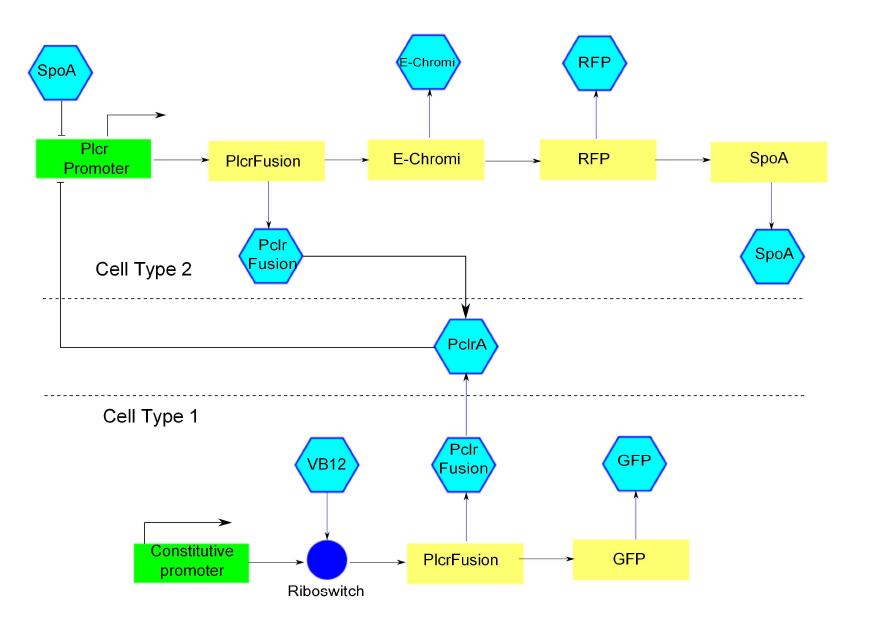
The intra cellular model is based on the block diagram shown in the figure below. The concentration of the proteins in the model can be expressed in terms of three ordinary differential equations.
Block diagram of the genetic circuit. Green rectangles represent promoters. Yellow rectangles represent genes. Blue hexagons represent inducer or activator proteins. Red hexagons are repressor proteins.
where
Methods and Tools
Extracellular Model
We will model the effects of our machine on the extracellular habitat by means of a system of differential equations. Measurements of the built machine as well as findings from the intracellular model will allow us to tweak parameters of this system to attempt to accurately determine the behaviour of the system. We will use Matlab \cite{Matlab} and Mathematica \cite{Mathematica} to help solve our system, to simulate and investigate the stability and properties of the system.
Intercellular Model (Cell Communication)
The network of cells and the communication between them is modelled in Matlab and its Simulink. \cite{Matlab} We treat each cell in the network as a black box that produces an output given an input based on data obtained experimentally and in conjunction with the intracellular model.
Intracellular Model (Gentic Circuit)
The modelling of the genetic circuit is done in CellDesigner. \cite{cellDesigner} \cite{art:CD1} \cite{art:CD2}. Through this application we can determine and specify all kinetic laws governing the system, on a reaction to reaction basis. We can also tweak each constant. These rate constants can be found in literature or experimentally if needs be. We can also provide simulations over given time periods with varying initial conditions for every component within the system.
Outcomes
We hope that the mathematical model of our genetic machine will allow insight into the desired effects and working's of the biological parts. From the model one will be able to establish boundaries to work within and utilize this to determine and guide biological choices.
Conclusion
The foundation set in place by a mathematical model are unrivalled in providing an understanding and insight to the nature of a system. Although first guesses may not be accurate from experimental data we can determine whether the model is fundamentally correct and requires fitting to the data, or if there is a fundamentally flawed assumption that overlooks an important aspect of the system. The importance of modelling this system is that we can determine initially how we hope the system will behave. From these initial guesses and hopes we can make educated choices in selecting biological mechanisms to function in a desirable way.
References
1.
2.
3.
 "
"