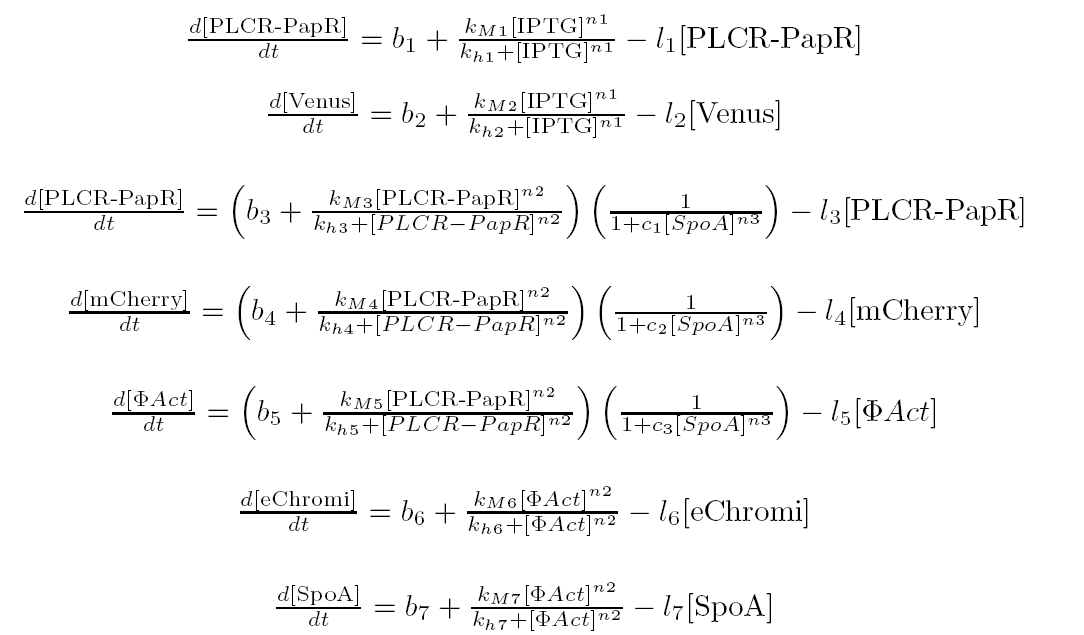Team:WITS-South Africa/Modelling
From 2010.igem.org
ByronJacobs (Talk | contribs) |
ByronJacobs (Talk | contribs) |
||
| (8 intermediate revisions not shown) | |||
| Line 63: | Line 63: | ||
We hope that the mathematical model of our genetic machine will allow insight into the desired effects and working's of the biological parts. From the model one will be able to establish boundaries to work within and utilize this to determine and guide biological choices. | We hope that the mathematical model of our genetic machine will allow insight into the desired effects and working's of the biological parts. From the model one will be able to establish boundaries to work within and utilize this to determine and guide biological choices. | ||
| - | + | == Results == | |
| + | The figure below show the concentration-time plot of the machine. There is a leakiness inherent with most promoters wherein the gene's are transcribed at a low constant rate without being activated. This introduces the problem of identifying correct operation of our machine or ruling out false positives. However given the increase in efficacy in production in the presence of an inducer we can regard the basal rates as an acceptable level of noise. | ||
| + | |||
| + | [[Image:UnactivatedBasal.png|950px|left]] | ||
| + | |||
| + | This figure below shows the effects of adding our input molecule IPTG. It is evident that the basal transcription rate is acceptable. | ||
| + | |||
| + | [[Image:ActivatedBasal.png|950px|left]] | ||
| + | |||
| + | === Discussion === | ||
| + | |||
| + | Experimental data will allow the model to be fit accurately. The efficacy of the promoters is increased substantially when in the presence of promoters, this allows us to guess, initially, that the basal rates are small and acceptable. The difficulty in this modelling is the behaviour of each genetic component, promoters for example, will behave differently from others and hence biological data is very specific and consequently is scarce in literature. Running experiments is the best way to generate accurate and applicable data, since the biology is known exactly. This is however a time consuming process and the results may vary. | ||
| + | |||
== Conclusion == | == Conclusion == | ||
| + | |||
| + | [[Image:DSC02486.JPG|450px|left]] | ||
The foundation set in place by a mathematical model are unrivalled in providing an understanding and insight to the nature of a system. Although first guesses may not be accurate from experimental data [[#References | [13]]] we can determine whether the model is fundamentally correct and requires fitting to the data, or if there is a fundamentally flawed assumption that overlooks an important aspect of the system. The importance of modelling this system is that we can determine initially how we hope the system will behave. From these initial guesses and hopes we can make educated choices in selecting biological mechanisms to function in a desirable way. | The foundation set in place by a mathematical model are unrivalled in providing an understanding and insight to the nature of a system. Although first guesses may not be accurate from experimental data [[#References | [13]]] we can determine whether the model is fundamentally correct and requires fitting to the data, or if there is a fundamentally flawed assumption that overlooks an important aspect of the system. The importance of modelling this system is that we can determine initially how we hope the system will behave. From these initial guesses and hopes we can make educated choices in selecting biological mechanisms to function in a desirable way. | ||
| Line 70: | Line 84: | ||
Although the derived kinetics used in the model are studied with respect to enzymatic reactions, the biological processes of gene expression and enzyme reactions have parallels that substantiate the use of these models. Literature, [[#References | [8]]] [[#References | [10]]] [[#References | [6]]], supports this assumption, by indicating similar behaviour and responses to activation although derived from a statistical perspective. This is promising outcome, and the prospect of better understanding the processes of genetic expression is a fruitful one. | Although the derived kinetics used in the model are studied with respect to enzymatic reactions, the biological processes of gene expression and enzyme reactions have parallels that substantiate the use of these models. Literature, [[#References | [8]]] [[#References | [10]]] [[#References | [6]]], supports this assumption, by indicating similar behaviour and responses to activation although derived from a statistical perspective. This is promising outcome, and the prospect of better understanding the processes of genetic expression is a fruitful one. | ||
| - | + | ||
| + | |||
| + | |||
| + | |||
| + | |||
==References== | ==References== | ||
| Line 114: | Line 132: | ||
16. Wolfram Research, I. (2008). Wolfram mathematica 7. Version: 7.0.0. | 16. Wolfram Research, I. (2008). Wolfram mathematica 7. Version: 7.0.0. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | = Modelling Presentation = | ||
| + | Below is the PDF presentation that was presented within the School of Computational and Applied Mathematics as part of the Honours Degree. | ||
| + | |||
| + | [[Image:IGEM_Presentation.pdf]] | ||
Latest revision as of 06:20, 27 October 2010

Contents |
Introduction
The biological sciences have generally been qualitative fields of study. However, due to the "top up" approach of synthetic biology, the need for quantitative mathematical models naturally arises. These models allow the biological system to be simulated and are necessary if control of the system is desired. We attempt to model a genetically engineered system implemented in the bacterium lactobacilus gasserii that is capable of detecting the presence of a pathogen, expressing a reported and also signaling others cells of the presence of the pathogen.
Project Outline
The aim of our machine is to identify an infection of Human papillomavirus in vivo. From a modelling point of view the mechanism has a number of points of interest expounded on in the following sections.
Extracellular Activity: Varying concentrations and effects of the genetic machine on the habitat outside the cell
Intracellular Activity: Responses to inputs and outputs as well as feedback loops
Intercellular Activity: A medium for communication between cells
Modelling
The benefits of modelling reach far beyond a theoretical understanding of a system. Models allow us to determine how we hope a system will behave. From this and experimental findings we can go on to determine where assumptions and simplifications made are critically important, whether it be positively or negatively.
Assumptions
- Total number of receptors, both occupied and unoccupied, is constant. [4]
- System reaches a quasi-steady state. [4]
- The number of input molecules is much greater than the number of receptors so that the receptors are always operating at maximal capacity. [4]
- We assume the number of operator regions is small with respect to the total number of repressor molecules. [15]
\end{itemize}
Components of the Model
Extracellular Model
The extracellular model describes the change in substances outside of the cell. These fluctuations are modeled by a system of differential equations, which are likely to be non linear and of an order higher than one. This model will be used to try and describe each cell as a 'black box'. This will then be used to model the intercellular communication.
Intercellular Model (Cell Communication)
This portion of the model describes the behaviour of the cells as a network of communicating individuals. They communicate via a signalling process called quorum sensing.
Intracellular Model (Genetic Circuit)
The genetic circuit describes the biochemical reactions taking place inside the cell. The intracellular model describes the fluctuations in concentrations of each substance by modelling each chemical reaction by means of an appropriate kinetic law.
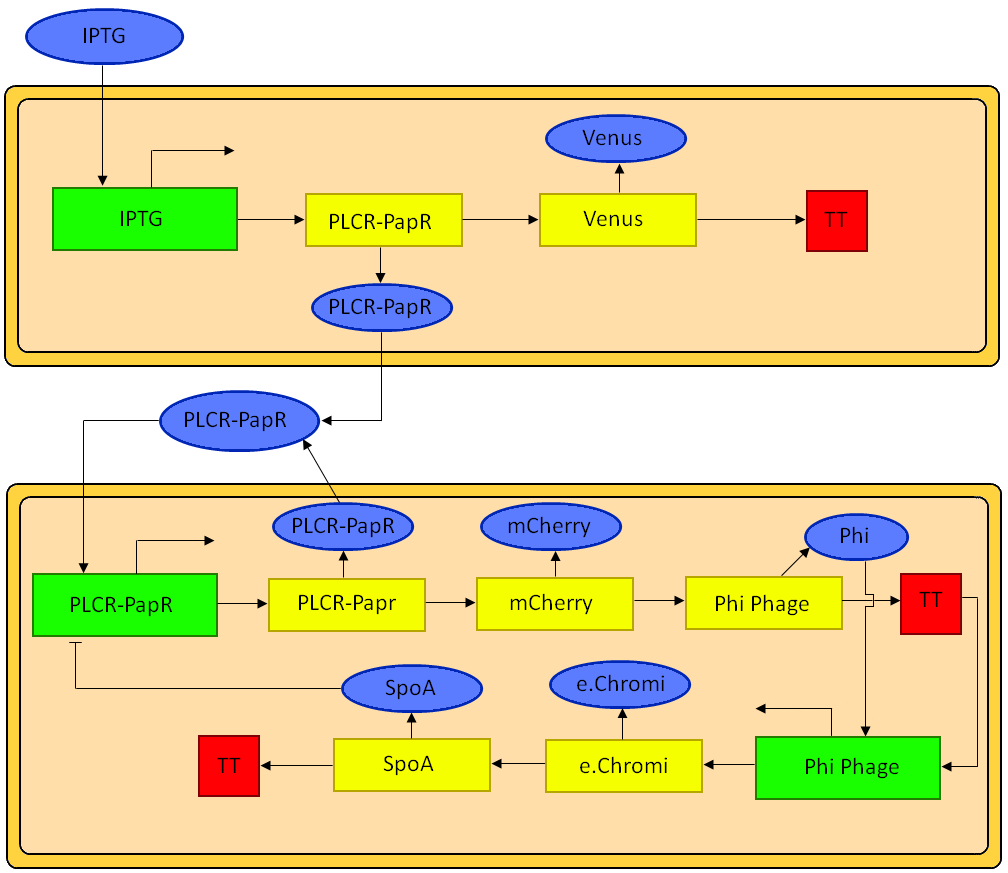
The intra cellular model is based on the block diagram shown in the figure below. The concentration of the proteins in the model can be expressed in terms of three ordinary differential equations.
Block diagram of the genetic circuit. Green rectangles represent promoters. Yellow rectangles represent genes. Blue ovals represent repressor, inducer or activator proteins. Red squares are terminator sequences.
Methods and Tools
Extracellular Model
We will model the effects of our machine on the extracellular habitat by means of a system of differential equations. Measurements of the built machine as well as findings from the intracellular model will allow us to tweak parameters of this system to attempt to accurately determine the behaviour of the system. We will use Matlab [9] and Mathematica [16] to help solve our system, to simulate and investigate the stability and properties of the system.
Intercellular Model (Cell Communication)
The network of cells and the communication between them is modelled in Matlab and its Simulink. [9] We treat each cell in the network as a black box that produces an output given an input based on data obtained experimentally and in conjunction with the intracellular model.
Intracellular Model (Gentic Circuit)
The modelling of the genetic circuit is done in CellDesigner. [2] [3] [14]. Through this application we can determine and specify all kinetic laws governing the system, on a reaction to reaction basis. We can also tweak each constant. These rate constants can be found in literature or experimentally if needs be. We can also provide simulations over given time periods with varying initial conditions for every component within the system.
Outcomes
We hope that the mathematical model of our genetic machine will allow insight into the desired effects and working's of the biological parts. From the model one will be able to establish boundaries to work within and utilize this to determine and guide biological choices.
Results
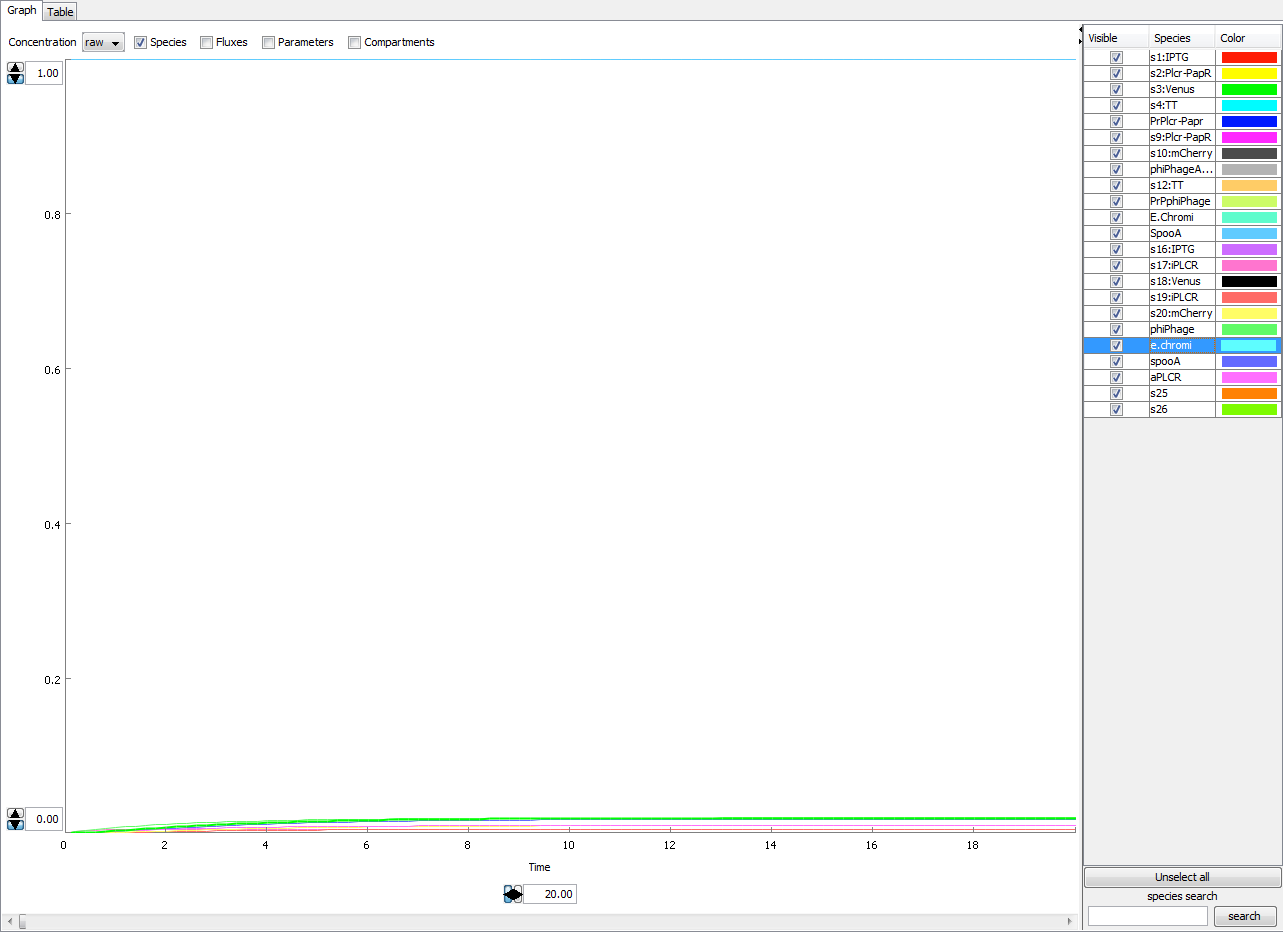
The figure below show the concentration-time plot of the machine. There is a leakiness inherent with most promoters wherein the gene's are transcribed at a low constant rate without being activated. This introduces the problem of identifying correct operation of our machine or ruling out false positives. However given the increase in efficacy in production in the presence of an inducer we can regard the basal rates as an acceptable level of noise.
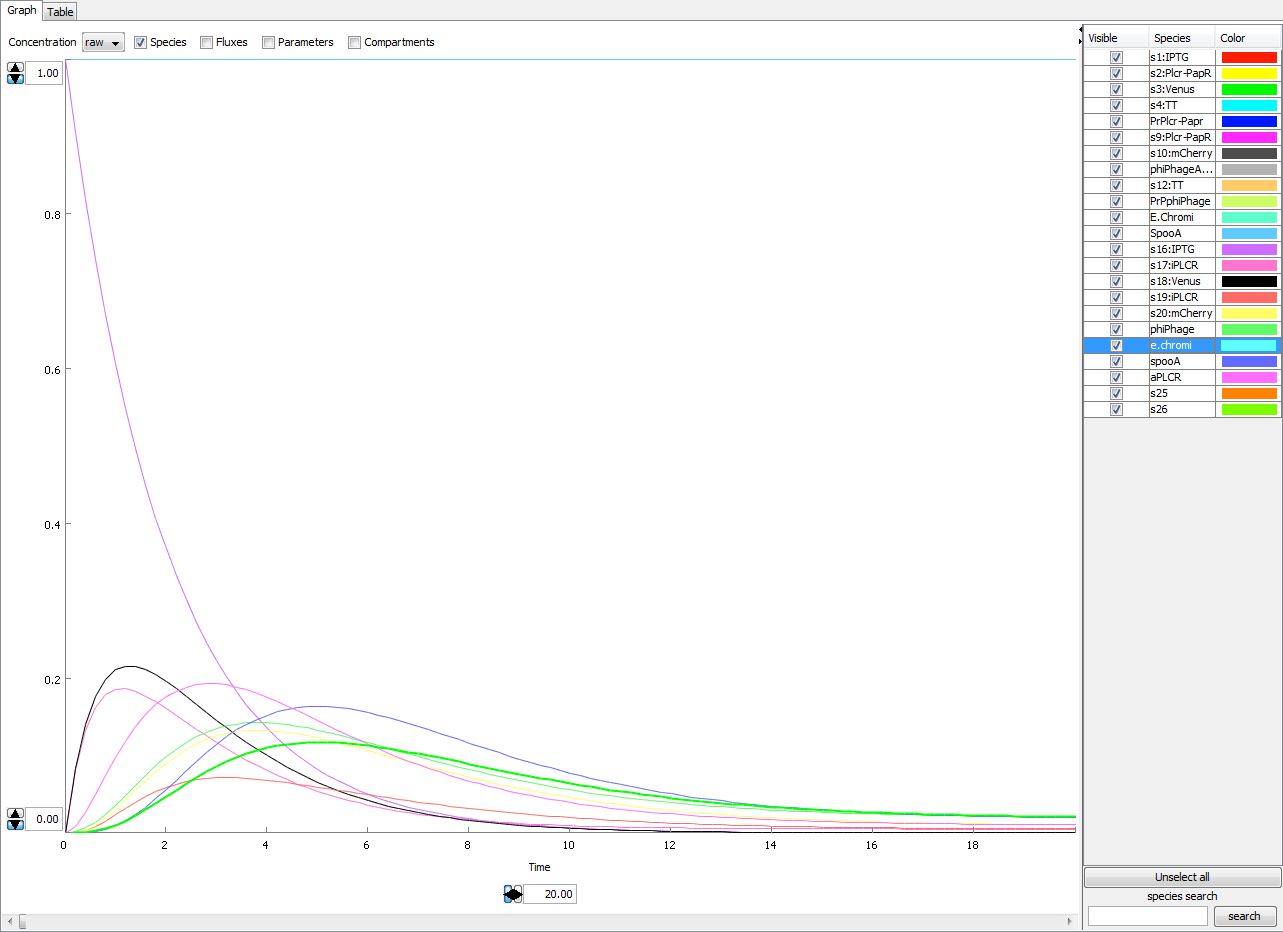
This figure below shows the effects of adding our input molecule IPTG. It is evident that the basal transcription rate is acceptable.
Discussion
Experimental data will allow the model to be fit accurately. The efficacy of the promoters is increased substantially when in the presence of promoters, this allows us to guess, initially, that the basal rates are small and acceptable. The difficulty in this modelling is the behaviour of each genetic component, promoters for example, will behave differently from others and hence biological data is very specific and consequently is scarce in literature. Running experiments is the best way to generate accurate and applicable data, since the biology is known exactly. This is however a time consuming process and the results may vary.
Conclusion
The foundation set in place by a mathematical model are unrivalled in providing an understanding and insight to the nature of a system. Although first guesses may not be accurate from experimental data [13] we can determine whether the model is fundamentally correct and requires fitting to the data, or if there is a fundamentally flawed assumption that overlooks an important aspect of the system. The importance of modelling this system is that we can determine initially how we hope the system will behave. From these initial guesses and hopes we can make educated choices in selecting biological mechanisms to function in a desirable way.
Although the derived kinetics used in the model are studied with respect to enzymatic reactions, the biological processes of gene expression and enzyme reactions have parallels that substantiate the use of these models. Literature, [8] [10] [6], supports this assumption, by indicating similar behaviour and responses to activation although derived from a statistical perspective. This is promising outcome, and the prospect of better understanding the processes of genetic expression is a fruitful one.
References
1. de Jong, H. (2002). Modeling and simulation of genetic regulatory systems: a literature review. Journal of computational biology.
2. Funahashi, A. and Kitano, H. (2008). CellDesigner 3.5: A versatile modeling tool for biochemical networks. Proceedings of the IEEE.
3. Funahashi, A. and Kitano, H. (2003). CellDesigner: A process diagram editor for gene-regulatory and biochemical networks. BIOSILICO.
4. Edelstein-Keshet, L. (1988). Mathematical Models in Biology. The Random House.
5. Gardner, T., Cantor, C., and Collins, J. (2000). Construction of a genetic toggle switch in escherichia coli. Nature.
6. Jack D. Dockery, J. P. K. (2001). A mathematical model for quorum sensing in pseudomonas aeruginosa. Bulletin of Mathematical Biology.
7. Jeff Hasty, David McMillen, J. J. C. (2002). Engineered genetic circuits. Nature.
8. Marc A. Suchard, Kenneth Lange, J. S. S. (2008). Efficiency of protein production from mRNA. Journal of Statistical Theory and Practice.
9. MathWorks, I. (2008). Matlab. Version: 7,7,0,471(R2008b).
10. Michal Ronen, Revital Rosenberg, B. I. S. and Alon, U. (2002). Assigning numbers to the arrows: Parameterizing a gene regulation network by using accurate expression kinetics. Proceedings of the National Academy of Sciences.
11. Michel Leno, O.-W. M. and Hache, J. (1992). Kinetic studies of cellular metabolic activity, specific igg production rate, igg mrna stability and accumulation during hybridoma batch culture. Enzyme and Microbial Technology.
12. Rubinow, S. (1975). Introduction to Mathematical Biology. Wiley-Interscience Publication.
13. Sarah Lebeer, Sigrid C. J. De Keersmaecker, T. L. A. V. A. A. F. K. M. and Vanderleyden, J. (2007). Functional analysis of luxs in the probiotic strain lactobacillus rhamnosus gg reveals a central metabolic role important for growth and biofilm formation. Journal of Bacteriology.
14. The Systems Biology Institute, Tokyo, J. (2010). Celldesigner. Version: 4.0.1.
15. Tyson, J. and Sachsenmaier,W. (1979). Depression as a model for control of the dna-division cycle in eukaryotes. Journal of Theoretical Biology, 79:275–280.
16. Wolfram Research, I. (2008). Wolfram mathematica 7. Version: 7.0.0.
Modelling Presentation
Below is the PDF presentation that was presented within the School of Computational and Applied Mathematics as part of the Honours Degree.
 "
"