Team:TU Delft/Modeling/MFA/explanation
From 2010.igem.org
MFA explained
Metabolic flux analysis (MFA) is a tool to study metabolic networks quantitatively. It can be used to calculate theoretical maximal yields.
Metabolic networks - definition
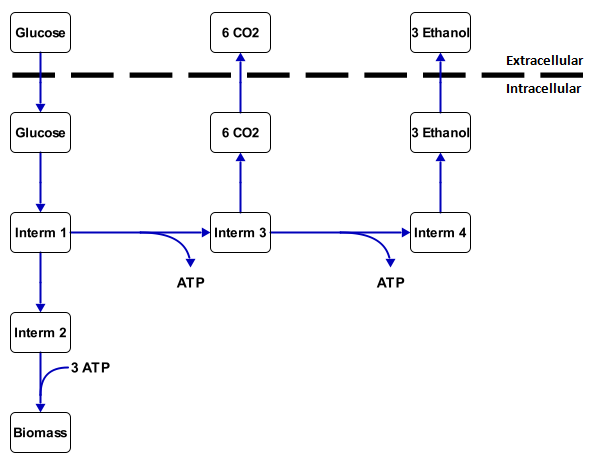
A metabolic network is the collection of all the reactions that occur inside a cell. All these reactions are coupled and form a network together. This network has a couple of transport reactions with substrate (food, such as sugar and alkanes) as an input and products (such as biomass, CO2, ethanol) as output. Other products of the metabolic network are energy, which is stored in molecules such as ATP and NADH, and building blocks for the cell (biomass). The substances between the substrates and the products are called intermediates. An example of this is in figure 1.
The change in the concentration of the substrate and products outside the cell can easily be calculated from measurements. This results in uptake and excretion speeds. The intracellular rates (inside the cell) can not be figured out as easily, but if enough information is known from the uptake en excretion rates, the intracellular rates can often be calculated.
Units in MFA
The term rate has occurred in the previous paragraph and needs to be specified further. Rates indicate how fast a reaction goes. Rates are usually defined in moles per amount of biomass per time. In CellNetAnalyzer the units mmol per gram of dry weight biomass per hour were used. The reaction that generates biomass, called μ, is an exception and has the unit per hour, which is derived from biomass produced per biomass per hour.
Steady-state assumption
In order to determine the intracellular rates, it is assumed that all the intermediates inside the cell are in a steady-state. This means that the amount of the substance is constant, meaning that the total production and the total consumption of a substance are equal to each other. This holds also for co-factors such as ATP and NADH which are used by many reactions. This means that all the rates need to have a ratio that balances out the co-factor production and consumption. This steady-state assumption for the co-factors has a very strong influence on how the fluxes are distributed through a metabolic network. The steady-state assumption does not hold for solid substances and extracellular substances.
Full flux determination
With this analysis all the intracellular fluxes are calculated to fit with a set of measured transport fluxes. For figure 1 this would mean that, if it is known that 1 mmol gx-1 h-1 of glucose is going in and 1.2 mmol gx-1 h-1 of CO2 is coming out, then the other rates can be calculated by working out all the mass balances. The calculation results in 1.32 mmol gx-1 h-1 of ethanol coming out and 0.36 mmol gx-1 h-1 goes through intermediate 2 to the biomass. This is essentially the metabolic flux analysis. For larger networks, however it is required to used linear algebra or tools such as CellNetAnalyzer.
Flux optimization
This is the analysis that is used in our iGEM project. This analysis does not try to calculated all the intracellular fluxes with a set of measured transport fluxes, instead it tries to optimize a (set of) fluxes to a set of transport fluxes. To calculate a maximal theoretical yield of a product on a substrate, the production rate needs to be optimized toward a certain substrate uptake rate. The yield of the product can the be calculated by taking the ratio of outflux of the product over the influx of the substrate.
Production by a metabolic network can be optimized with a built in function of CellNetAnalyzer. This function will calculate with a given set of substrate inflows the maximal rate for a product. An advantage of this is that not all the transport rates need to be known, the function simply finds an optimal solution.
For example, say that there there is a inflow of 1 mmol gx-1 h-1 substrate in the network of figure 1 and the rate for ethanol needs to be maximized. The function will then assign values to all the reaction rates to make the outflow of ethanol as large as possible, while still fulfilling all the steady-state conditions. For this example the outflow of ethanol will be 1.8 mmol gx-1 h-1. The rest goes into biomass. The maximal yield is then 1.8 mol ethanol per mol substrate. A more accurate yield for carbon based substrates and products is a yield in Cmol product per Cmol substrate. If this value is 1 and there is only one carbon substrate, then all the carbon atoms from the substrate are directed into the product. Glucose has 6 carbon atoms and ethanol has two carbon atoms. The yield then becomes 0.6 Cmol ethanol per Cmol of glucose.
It is also possible to optimize the growth by maximizing μ. If there is no feasible solution for this, then the cell is not viable because it can not use the substrate for growth. This may occur for example when a lot of NADH is produced, but cannot be consumed sufficiently somewhere else in the network because of anaerobic conditions. Because of this the network cannot maintain the steady-state condition. This situation is called redox stress.
Click here to read about how the metabolic network was constructed for this project
Click here to go back to the MFA main page
 "
"