Team:St Andrews/project/modelling/model 1
From 2010.igem.org
| Line 2: | Line 2: | ||
= Model 1: Single Cell without Feedback = | = Model 1: Single Cell without Feedback = | ||
| + | |||
== Theory & assumptions == | == Theory & assumptions == | ||
Revision as of 16:14, 7 September 2010


Model 1: Single Cell without Feedback
Theory & assumptions
The first method we attempted was to put the user in control of the change in HSL within the cell, and take any HSL produced and remove it from the system entirely. In this fashion a gradual increase in cell density was simulated by a linear “ramp up” of the HSL in the cell; a gradual decrease (presumably due to cell death) was simulated by a linear “ramp down” in HSL. The activation of the cell was measured by plotting the GFP concentration.
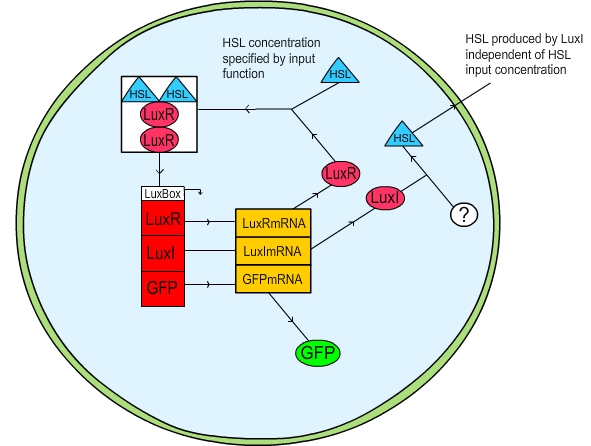
Figure 1: Schematic diagram of the LuxR quorum sensing circuit
Results
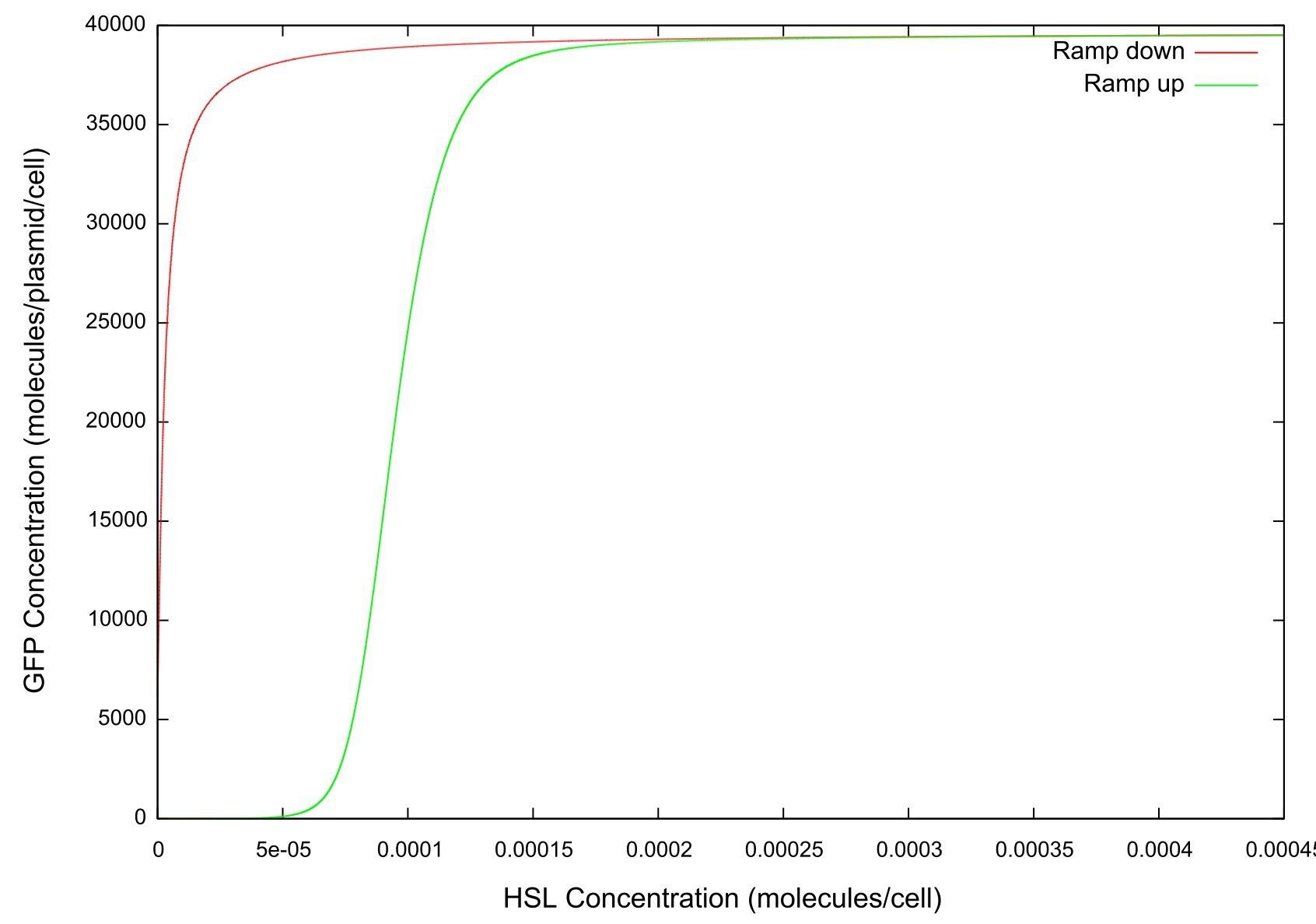
In order to simulate the effect of the cell colony growing in number we first set the change in HSL concentration to a fixed value and ran the model until a steady state was reached. It can be clearly seen from figure . that the level of GFP in the cell reaches a point where the concentration starts to sharply increase before a plateau is reached and there is no further activity. This is the switch-on, where the cell has moved from a down-regulated to an up-regulated state and starts to produce greater amounts of HSL, LuxR, LuxI and GFP.
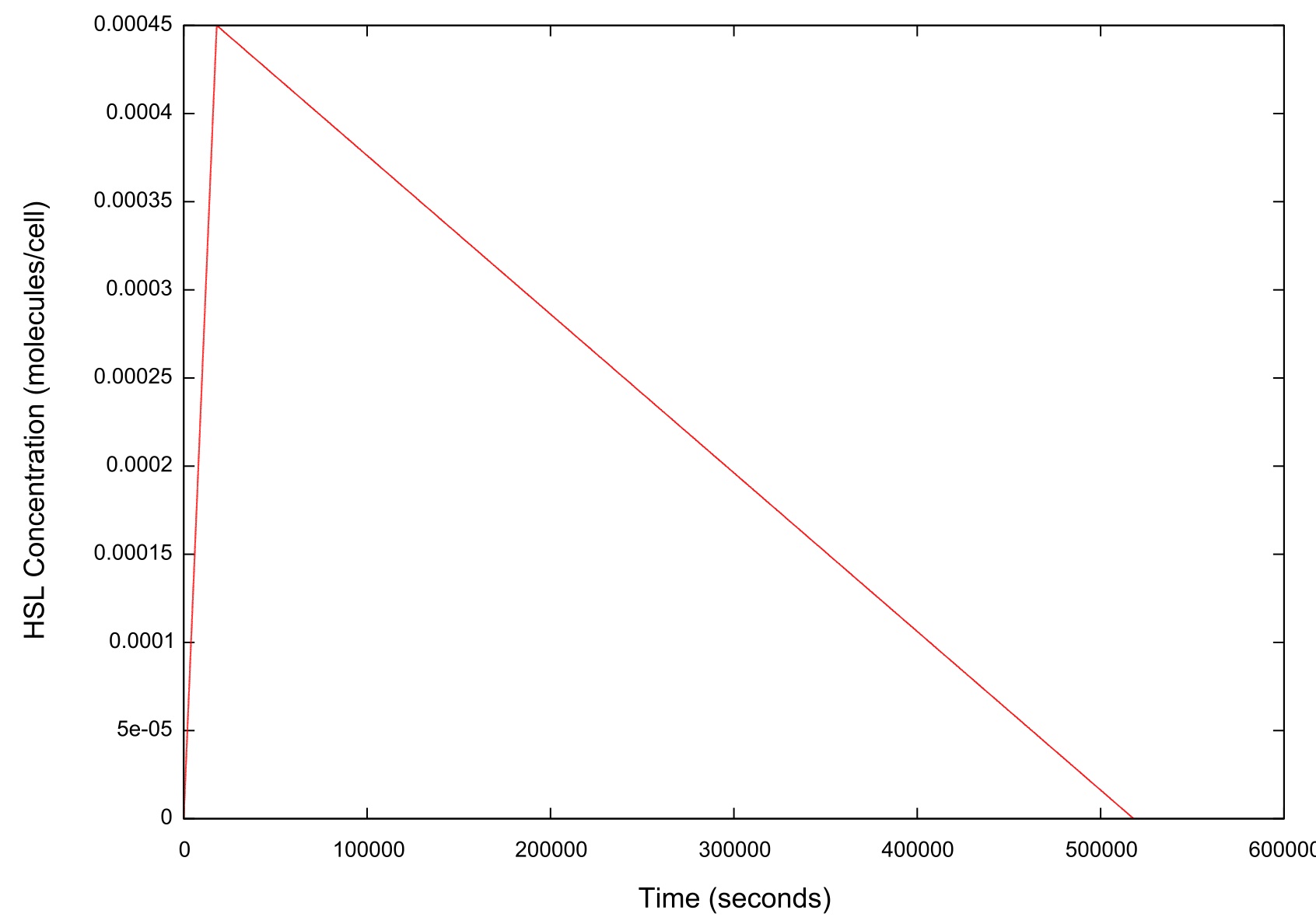
Figure 2: Graph of the HSL input over time
As figure 2 shows, when ramping the HSL down we chose a rate which was significantly slower than that used when performing a ramp up in HSL.
Figure 3: Graph of GFP v HSL
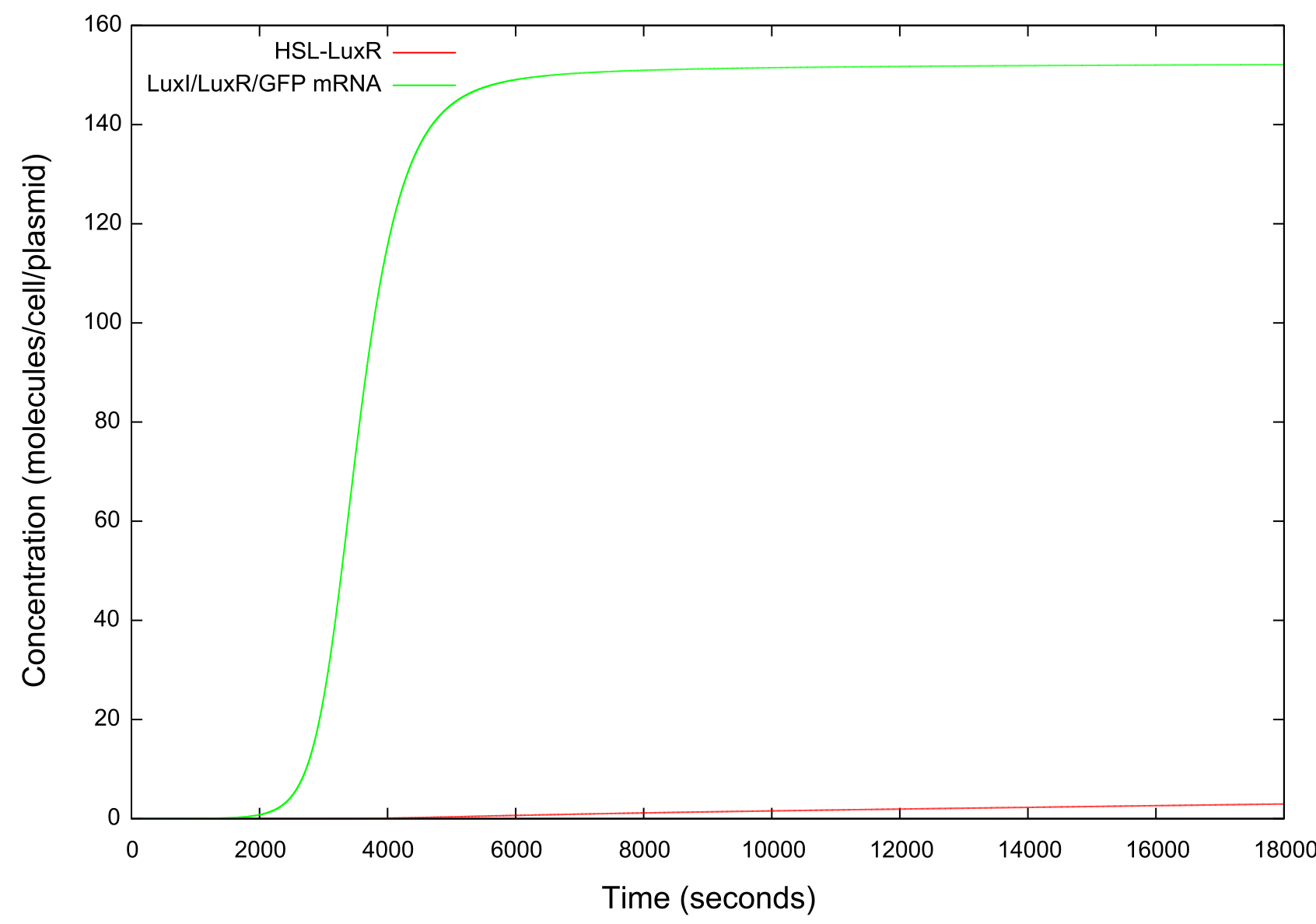
The final values of all the molecules are RNAs are then substituted into the model as the initial values for the next run and the HSL is reduced at a fixed rate, producing the data shown in figure . It can be seen that the up-regulation is maintained for a much lower HSL threshold than when the first run. In fact, the cell never fully returns to a down-regulated state again. After trying to achieve this through decreasing the rate at which the HSL is taken away and increasing the number of increments for which the model is run, it was decided that our model simply did not produce the behaviour we were looking for. Figure shows how the concentrations of the various molecules and the mRNAs changes over the transition from down- to up-regulated states. The model predicts low concentrations of the HSL-LuxR complex which is theoretically predicted, but in general the results were unsatisfactory as to drawing any real conclusions about the causes or otherwise of the bistability.
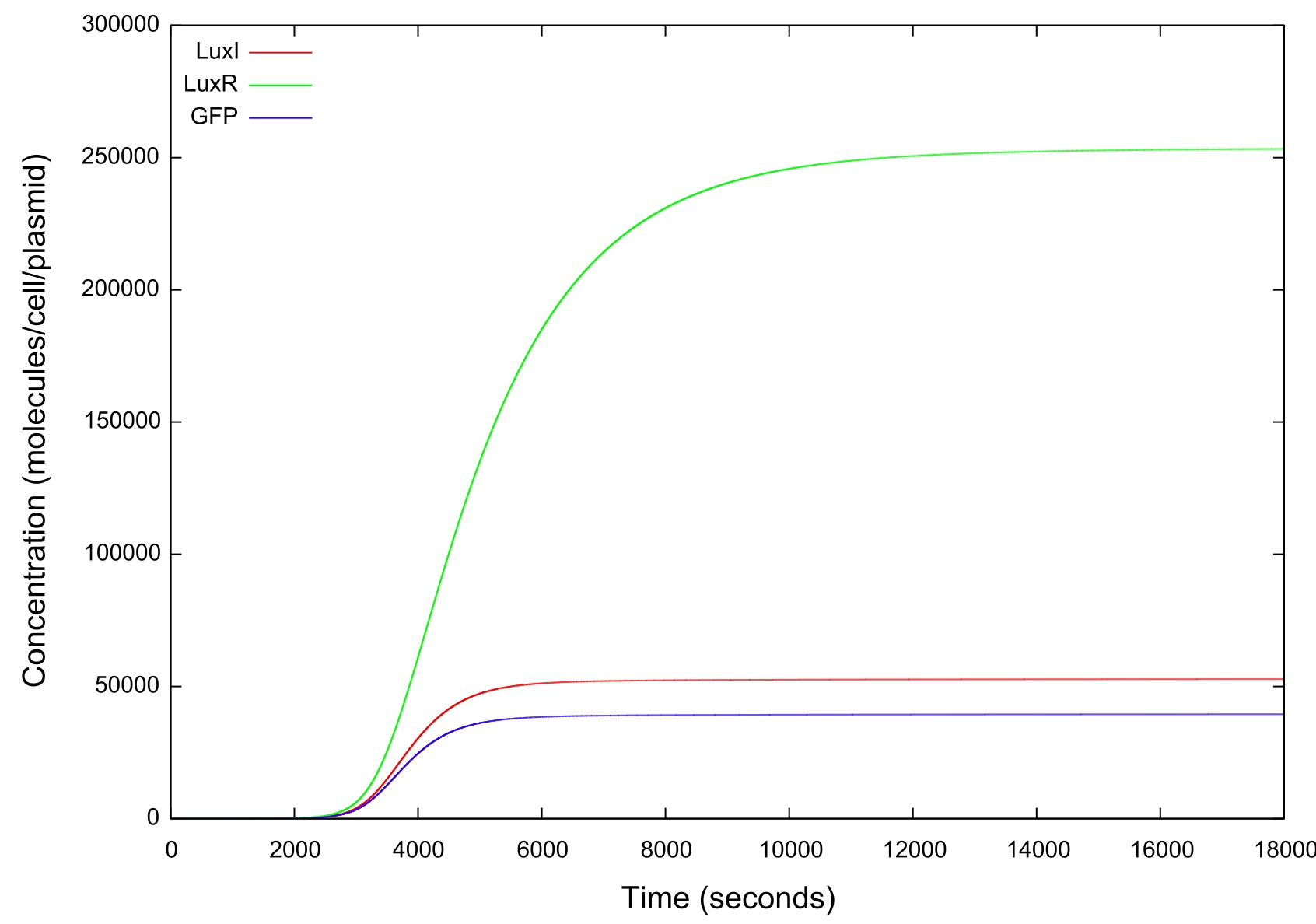
Figure 4: Graph showing the variation in the concentrations of all the components of the system with time during the HSL up ramp
It should be noted that while figure 4 actually contains plots of the mRNA concentrations and of the HSL-LuxR complex, they are so small when compared to the other components that they cannot be appropriately scaled.
Figure 5: Graph showing the change in concentrations of HSL-LuxR and mRNA with time over the HSL up ramp
 "
"