Team:Slovenia/PROJECT/oscillator/smolen/results
From 2010.igem.org
| Line 41: | Line 41: | ||
#vsebina_mid{ | #vsebina_mid{ | ||
| - | height: | + | height: 4429px; |
} | } | ||
#lgumb4{ | #lgumb4{ | ||
Revision as of 00:15, 28 October 2010
Contents |
Deterministic model - overview
As already mentioned, deterministic model is based on a system of ordinary differential equations, which needs to be solved. Deterministic model was implemented in the MATLABs toolkit SimBiology. The following differential equations were used (pT7* denotes the activated promoter, while pT7' is repressed promoter):
1. plasmid (T7 RNA polymerase under the control of T7 promoter and T7 RNA polymerase under the control of constitutive cytomegalovirus promoter):
2. plasmid (transcriptional repressor NICTAL under the control of T7 promoter):
3. plasmid (yellow flourescent protein Venus under the control of T7 promoter):
MATLAB SimBiology project file (SBML) for this model can be found here. You can find how to set up the simulation in simbiology here.
Deterministic model - results
The following initial parameters were used for the simulation. Values represent relative concentration units, ratios were considered in later biological experiments:
[pT7_rnapt7] = 1
[pT7_ZNF] = 20
[pT7_gfp] = 2000
[pCMV] = 1
All other initial concentrations were set to 0.
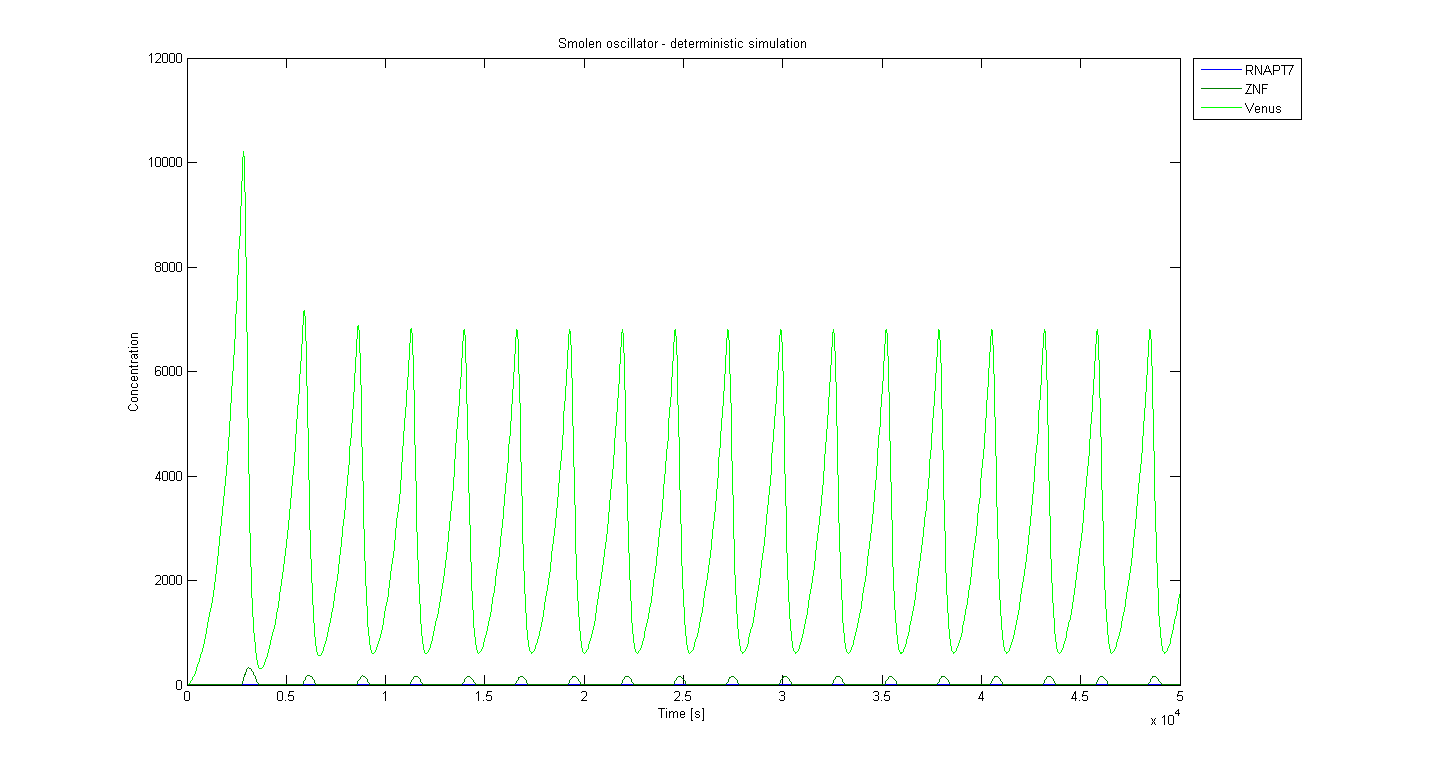
The base period of this simulation is around 2700 seconds, which is approximately 45 minutes. Model shows that longer periods (meaning lower frequency) can be achieved by adjusting the concentration of ZNF or T7 RNA polymerase under the control of T7 promoter. The first higher peak is due to the ramp-up of oscillator and it appeared in every simulation we ran. Note that these graphs show the concentration of the actual product of the reporter and not the repressed or activated promoters.
Stochastic model - Overview
Same chemical equations, constants and kinetic rates were used as in deterministic model. The script for MATLAB can be found here, while the input file for SGN Sim can be found here. Detailed explanation of what these two files contain is here.
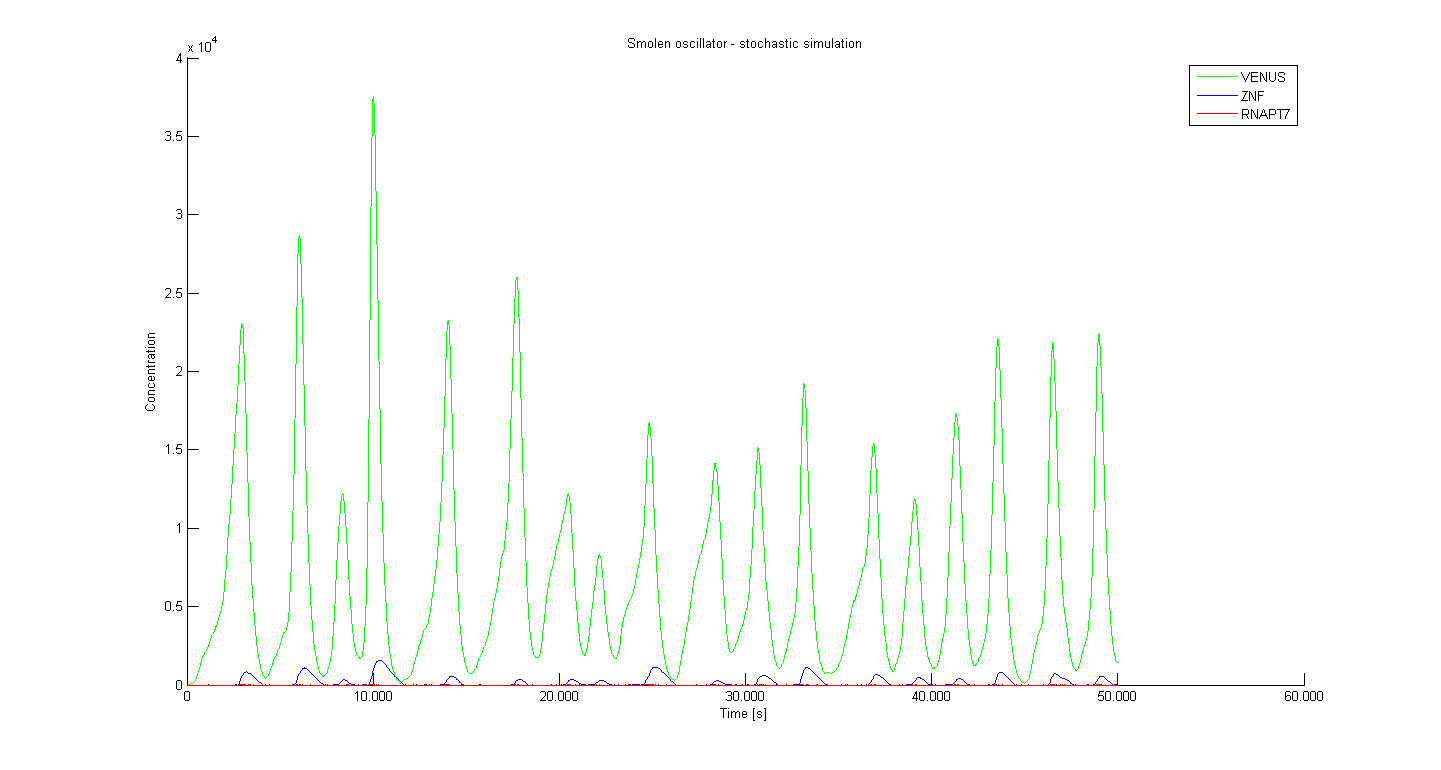
Stochastic model - Results
Several different initial parameter values were used in order to see what happens with the system if we were able to adjust the degradation of repressors or if we adjust the amount of the initial promoter concentration. Figure 1 bellow presents the results obtained using parameter values that were the same as in our deterministic simulations.
Results are in accordance with our deterministic simulation, however stochastic simulation is a better approximation of the real system as it include the 'random' nature factor. The period from stochastic simulation is little over 3000 seconds, which is approximately 50 minutes.
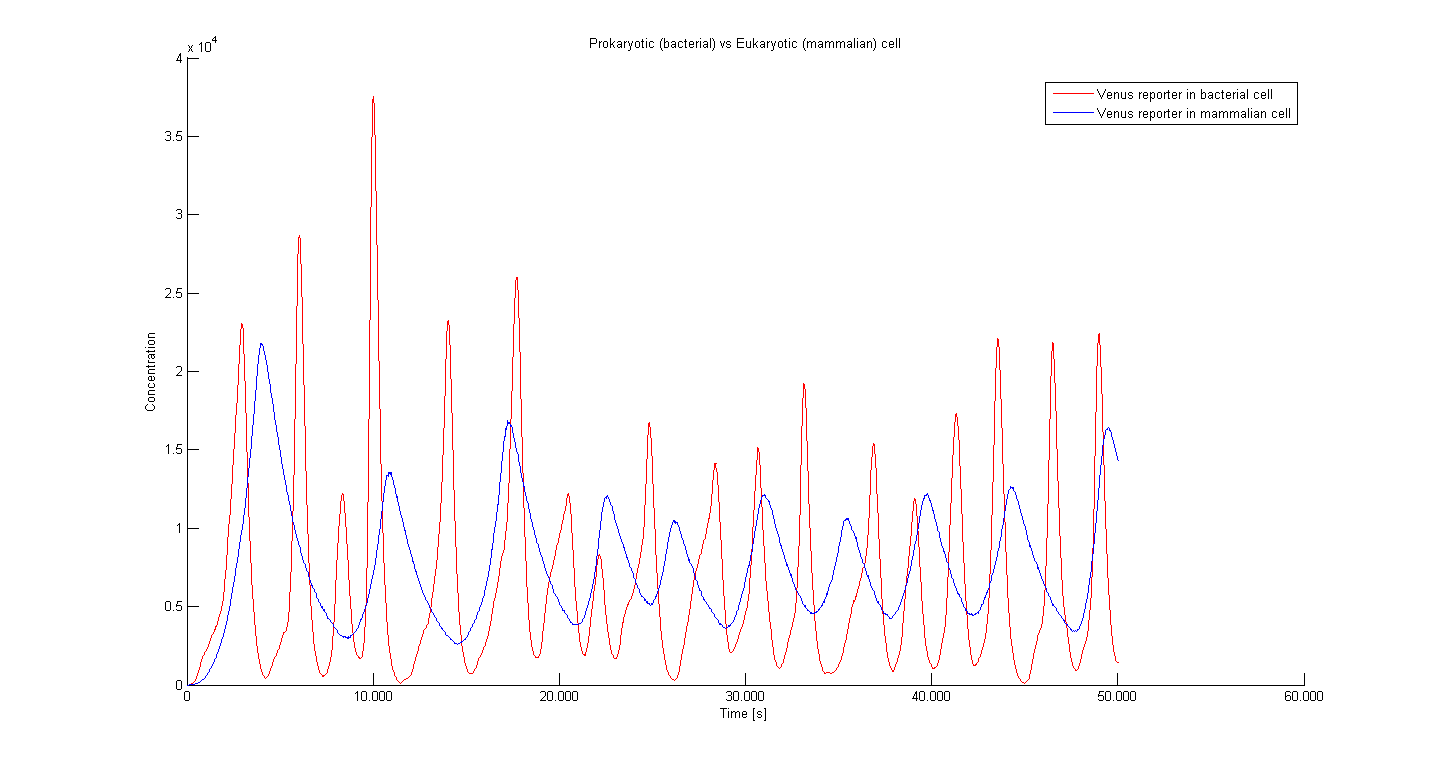
The period of oscillation in eukaryotic cells is longer due to the delay between transcription and translation.
Both deterministic and stochastic simulations give similar results. Because Smolen oscillator is quite simple, the period length is shorter compared to repressilator.
 "
"