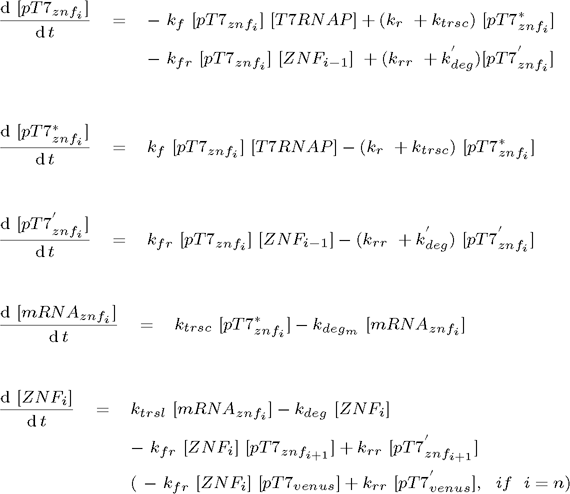Team:Slovenia/PROJECT/oscillator/represilator/results
From 2010.igem.org
Contents |
Deterministic model - overview
As already mentioned the system of ordinary differential equations completely describes the deterministic model. Deterministic model for the version of repressilator based on zinc finger repressors was written for MATLABs toolkit SimBiology and is determined by the following differential equations (pT7* denotes activated promoter, while pT7' is repressed promoter):
The MATLAB project file (SMBL) for SimBiology is available here. You can find how to setup the symbiology simulation here.
Deterministic model – repressilator with increased number of repressors in the cycle
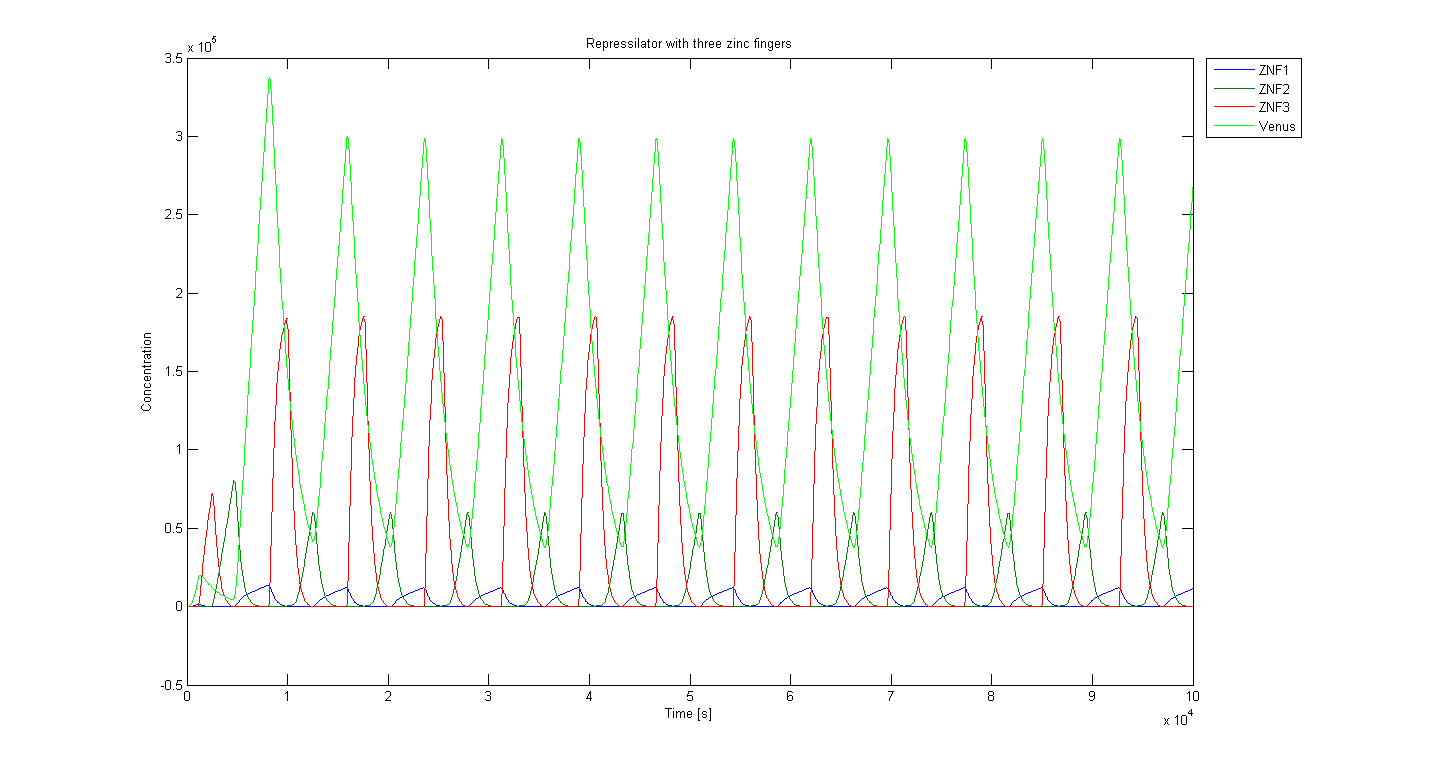
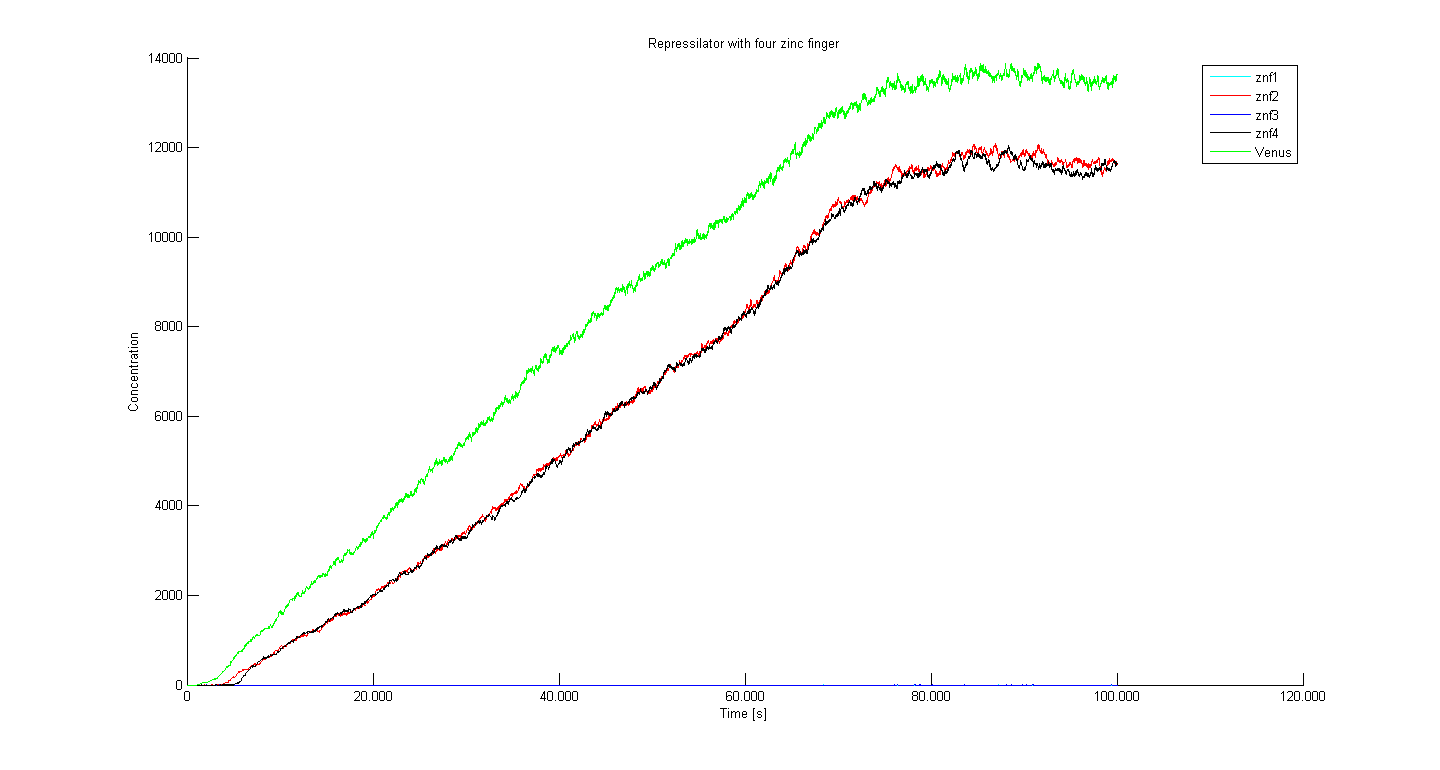
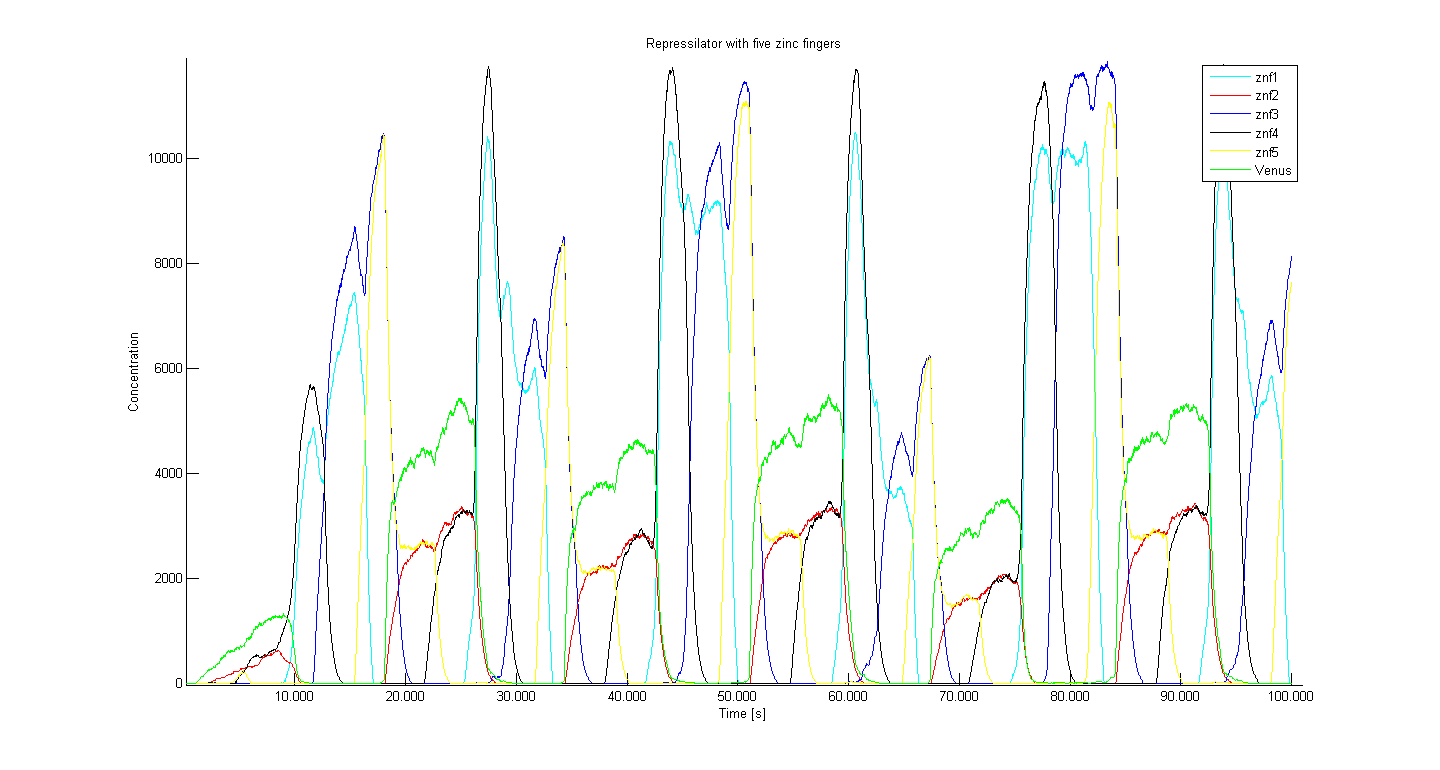
Three different setups of simulations were done (repressilators comprisong three, four and five zinc fingers).
Comparing the 3 zinc finger (Figure 1) and 5 zinc finger repressilators (Figure 3), we can see that the period of oscillation roughly doubles. The reason is that the longer 'cycle' it has to do steps 1-3-5-2-4-1-... compared to 1-3-2-1-...
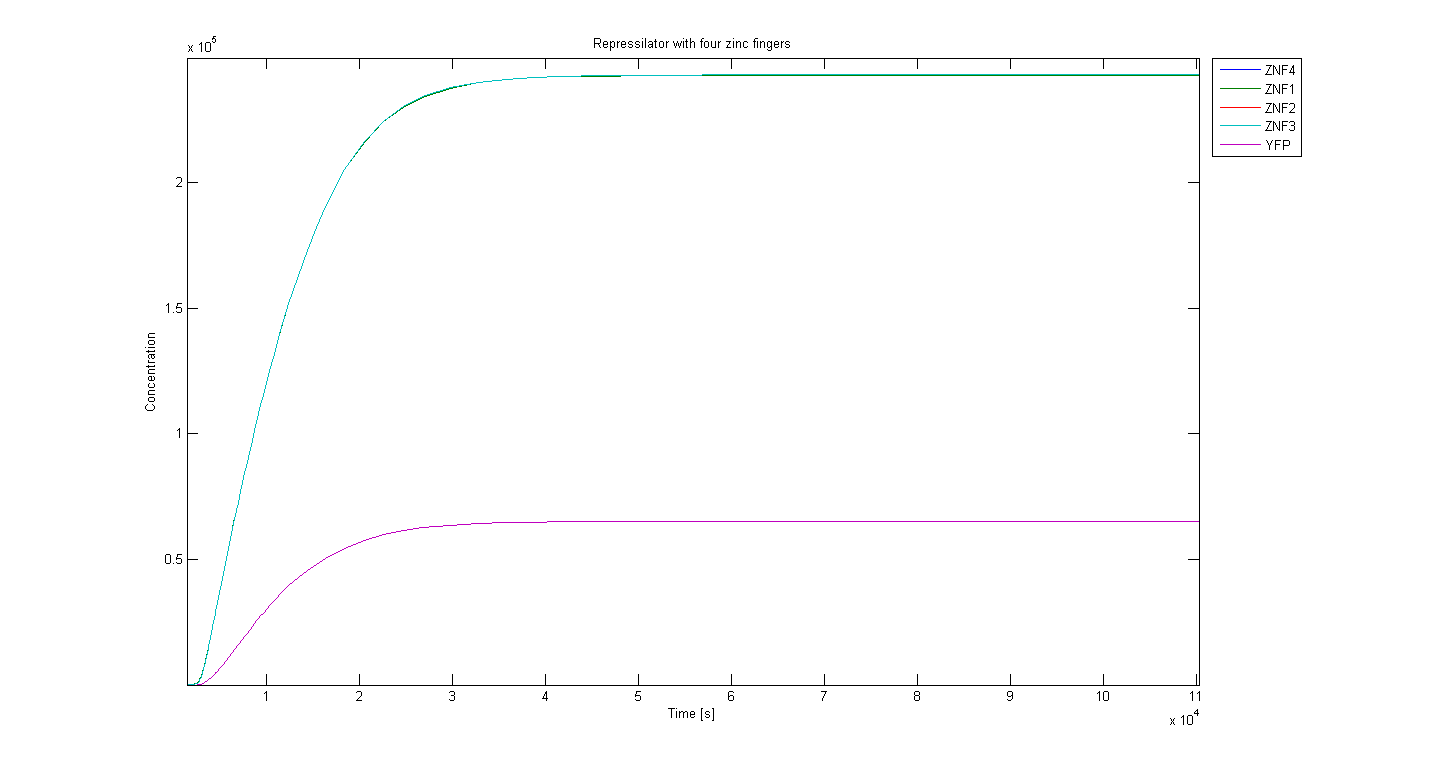
Our results also confirm that stable oscillation occur for the odd number of repressors. An even number produces a stale-mate situation, where the first zinc finger that manages to increase (which is determined by the zinc finger repressing the reporter as it recruits a certain amount of a particular zinc finger) will never be repressed (Figure 2). That happens because the circle in an even-numbered repressilator connects before production of all zinc fingers is repressed (for 4 zinc finger repressilator: either 2-4-2-4-.. or 1-3-1-3-.. ; where numbers indicate the unrepressed zinc fingers) and only the zinc fingers that are not in the circle are being repressed while others rise to an equilibrium. Odd number repressilator cannot enter into such a state (unrepressed zinc fingers for 5 zinc finger repressilator: 1-3-5-2-4-1-3-...), because production of every zinc finger is repressed eventually.
Stochastic model - overview
There are several benefits of using SGN Sim. The input file for the simulation is much simpler. Implementation of the model is thus much faster and it is also much easier to understand it compared to MATLAB script file. Moreover it takes less time to perform a simulation. Therefore only SGN SIM was used for the stochastic simulation of the repressilator.
The input file for SGN Sim can be found here. The explanation of the file can be found here.
Stochastic model - results
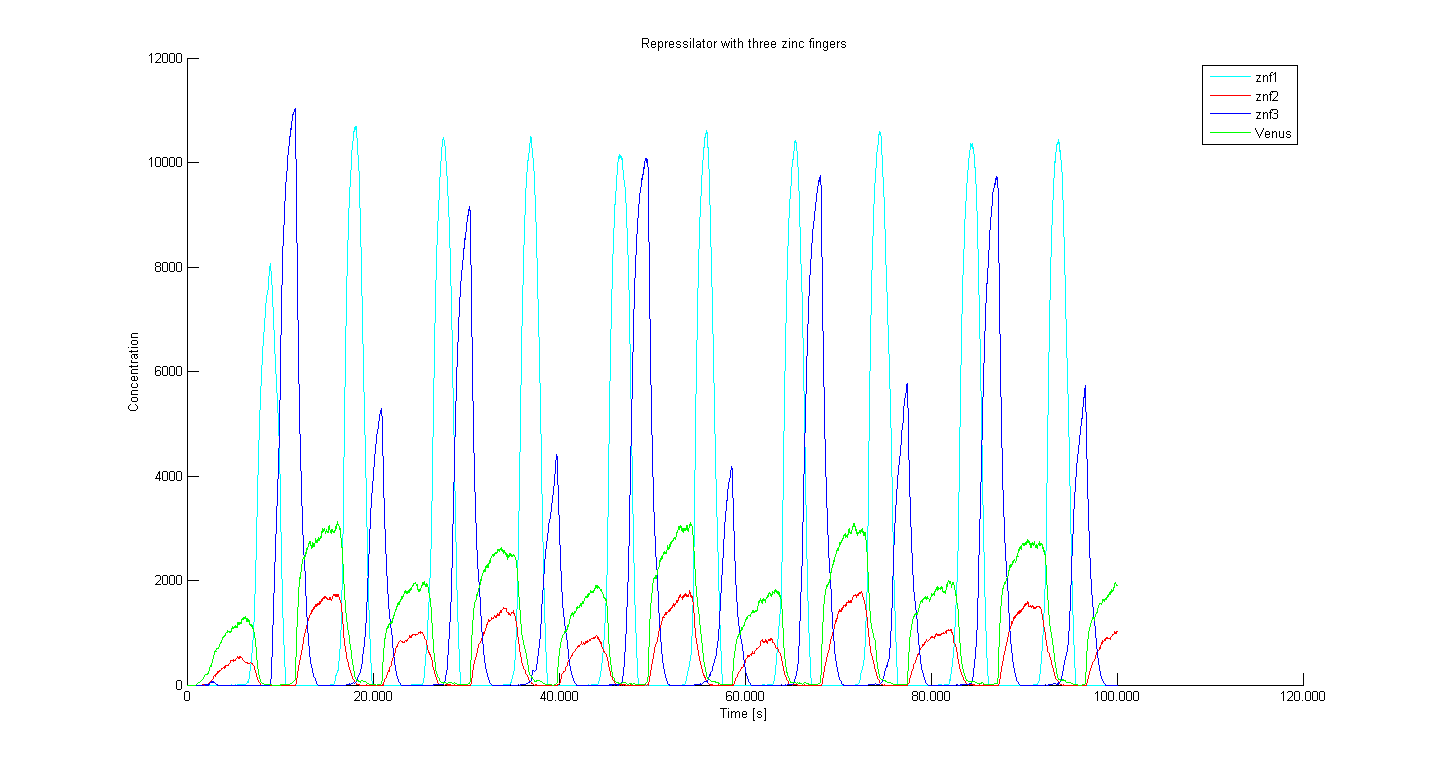
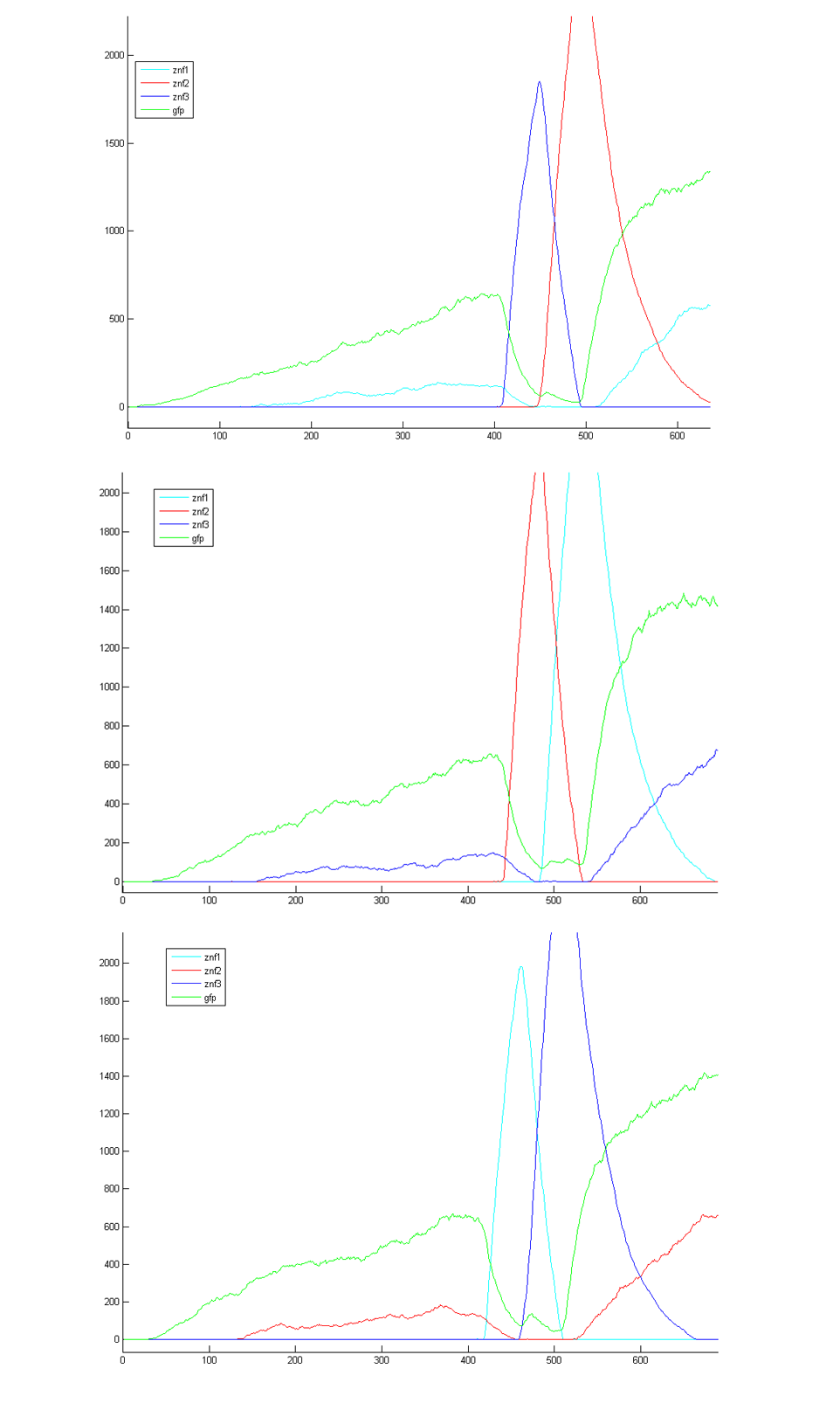
Three different initial parameter values simulated in the deterministic model were also used in the stochastic model (three, four and five zinc fingered cycles). Every simulation is represented with two figures, the first one showing the entire simulation and the second showing how the start of oscillation. The start of oscillation is important, since our model shows that it is determined bythe zinc finger that acts as a repressor to the reporter gene. Following that logic, the start of oscillation in a repressilator without the reporter gene should be random. Three performed simulations without the reporter gene confirm that. On the other hand if the genome contains the binding site for a certain zinc finger its effective concentration would be affected as well and this could reflect on the outcome. This is very relevant for zinc fingers recognizing 9 nucleotides but much less for the zinc fingers recognizing 18 nucleotides as their binding site are not likely to occur even in the complex genome.
Figures show that the results of stochastic model are fairly similar to the ones of deterministic model. For example the oscillation period for 5 zinc finger deterministic model is 15000 seconds and for 5 zinc finger stochastic model is 16000 seconds.
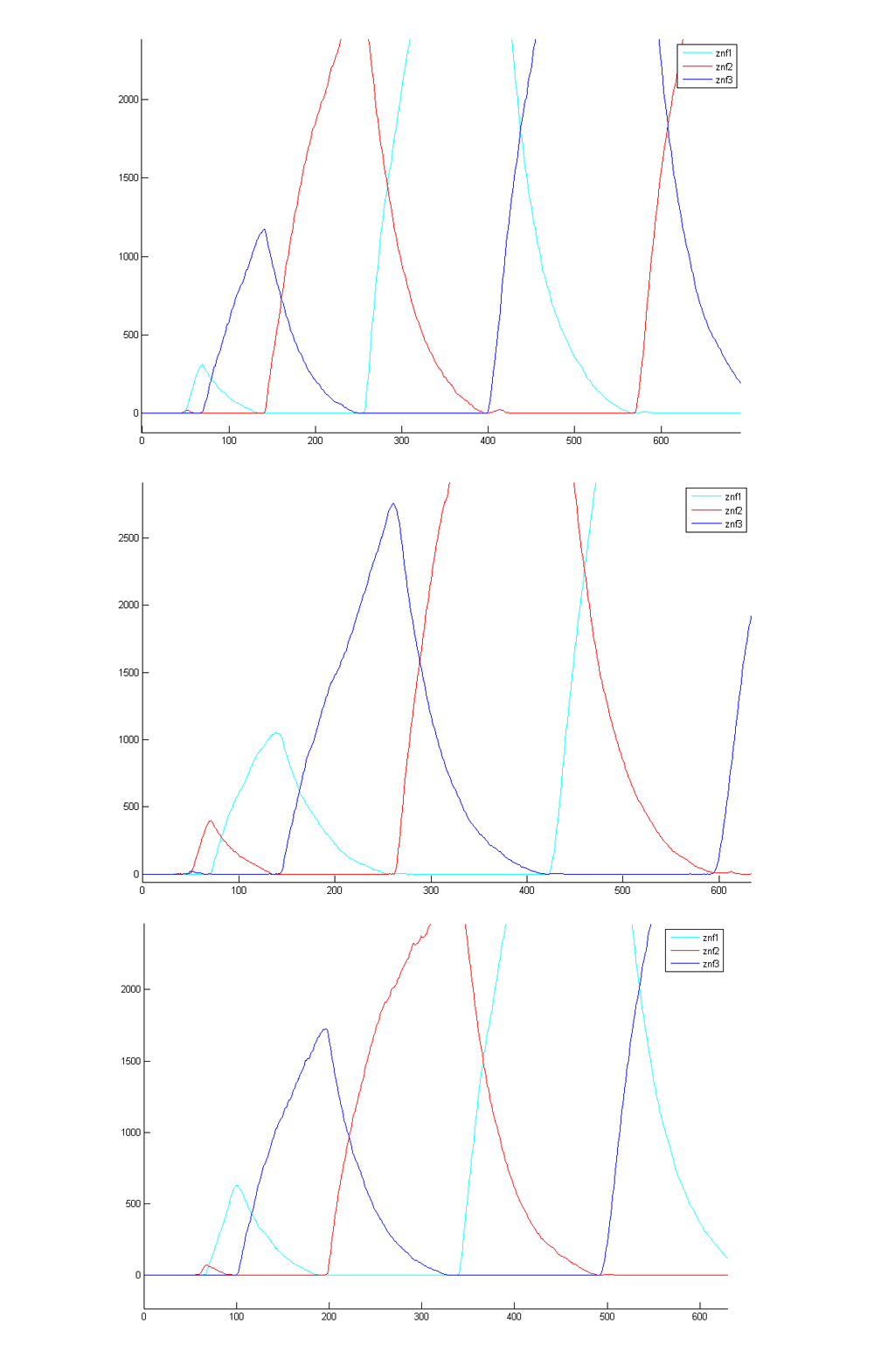
Figure 2 shows that no oscillation occurs when we have even number of zinc-finger proteins, since the system is in a stale-mate situation where two zinc fingers are consistently repressed, while the other two rise.
Stochastic model confirms that having more zinc fingers in the system increases the period and lowers the frequency of oscillation in a predictable way, since it takes longer for repression cycle to connect.
Figures of the magnified oscillation start show that the start of oscillation is determined by which zinc finger protein is repressing the reporter gene. Because it has to repress both production of reporter and the zinc finger protein that is next in the sequence, the gene repression of the this next zinc finger protein is weaker, which leads to higher production and rise of the first oscillation. Figure 4 shows three different simulations with same initial parameter values, they all start with the same zinc-finger protein rising first, figure 5 shows that if we change the repressor of reporter gene, the start of oscillation also changes. Figure 6 confirms that if there is no reporter gene in the system, the start of the oscillation is random - three different simulations resulted in three different starts.
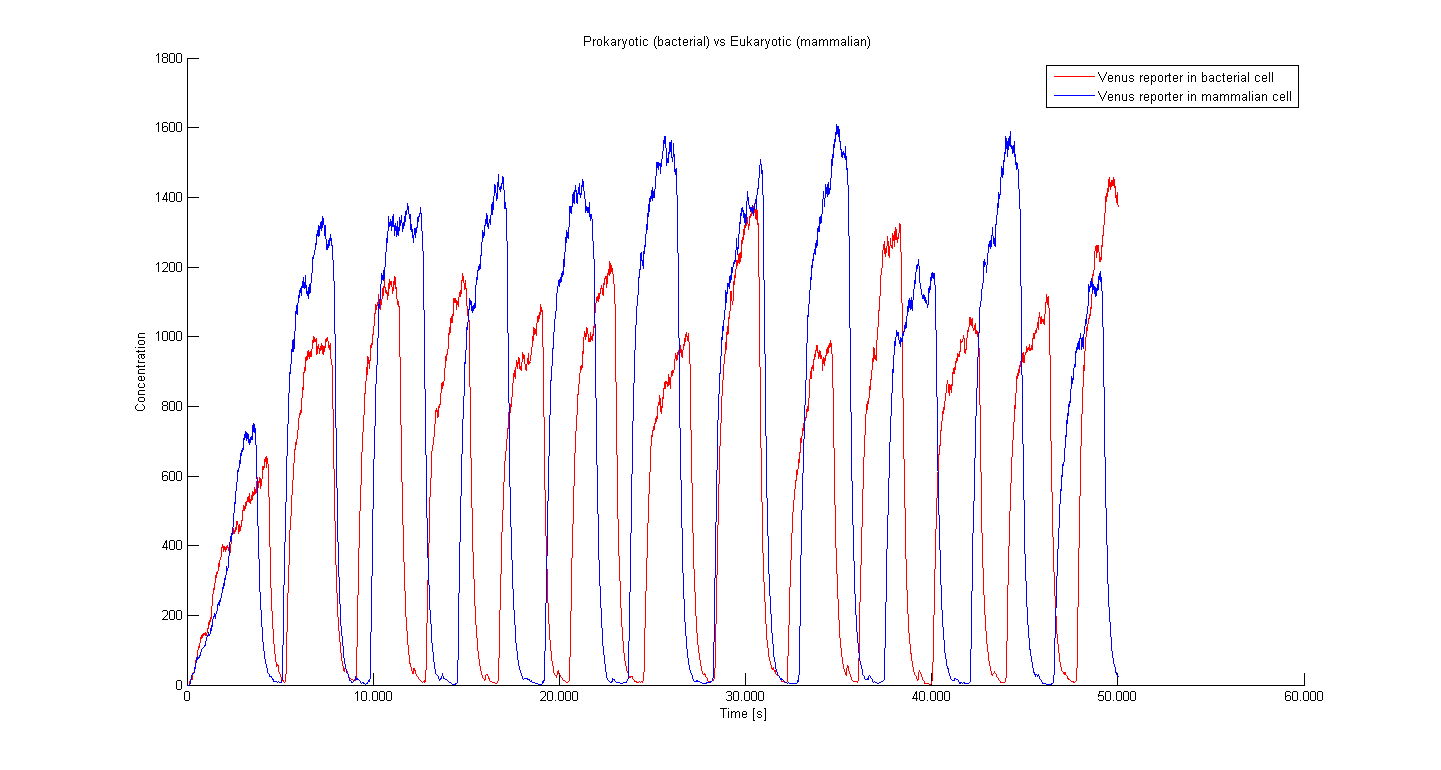
Figure 10 shows the difference between prokaryotic (bacterial) and eukaryotic (mammalian) cells. The main difference is again in the delay between transcription and translation, which results in a little longer period for eukaryotic cells.
Our simulations showed that only odd number zinc finger system produce oscillations. If we use even number zinc finger system only half of them will get repressed. Simulations also suggest a difference in the period of oscillations if we compare prokaryotic and eukaryotic cells.
 "
"