Team:Northwestern/Project/Modeling
From 2010.igem.org
| Home | Brainstorm | Team | Acknowledgements | Project | Human Practices | Parts | Notebook | Calendar | Protocol | Safety | Links | References | Media | Contact |
|---|
|
| ||||||||||||||||||||||||||||||||||||
ObjectiveThe main purpose of modeling was to characterize the topography of the kinetics behind foreign protein/product production in recombinant E.Coli biofilm with a diffusing inducer, and the effect on the various species involved by primarily the following factors:
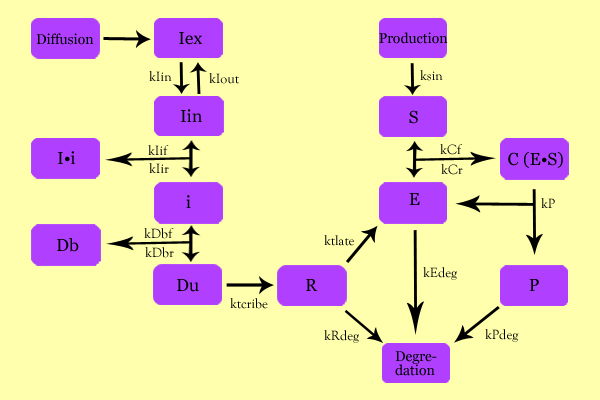
ModelingOverall ModelUsing enzyme kinetics equations, we elected to mathematically simulate the following model:
Variables
EquationsThe differential of the variables were found as follows:
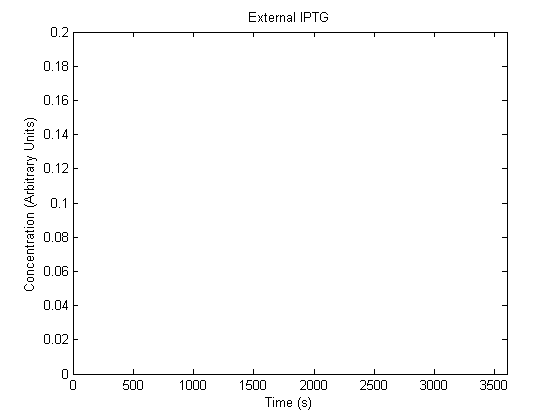
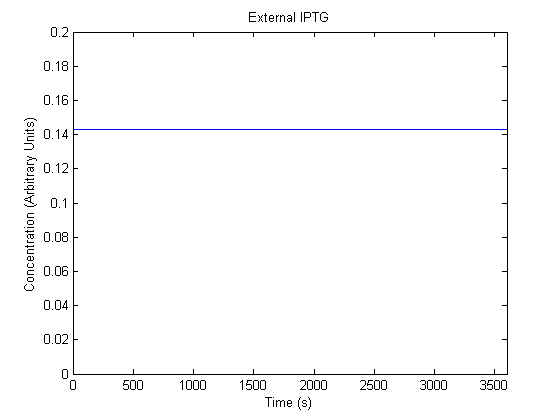
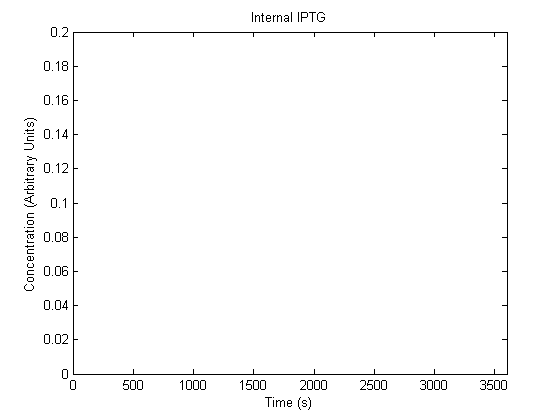
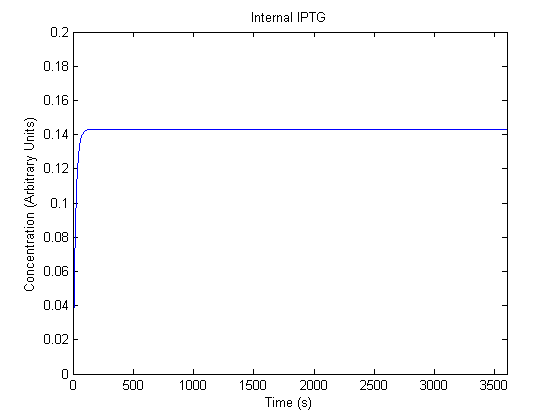
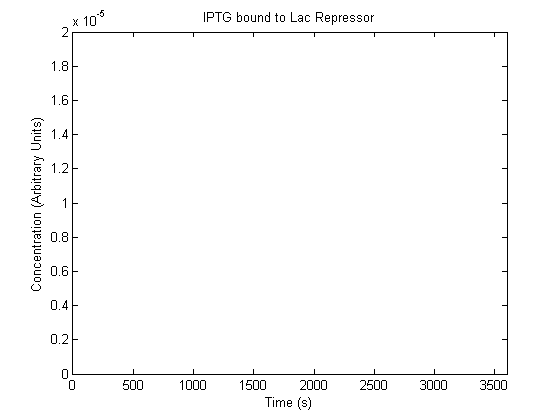
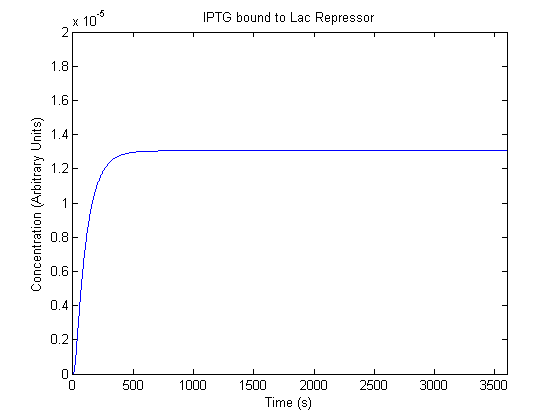
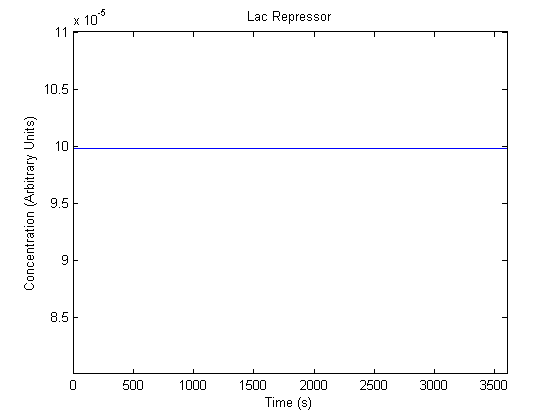
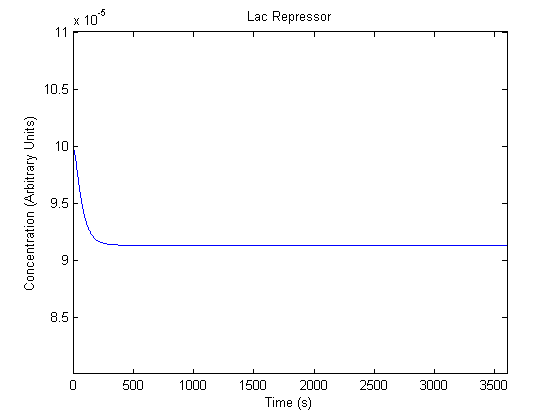
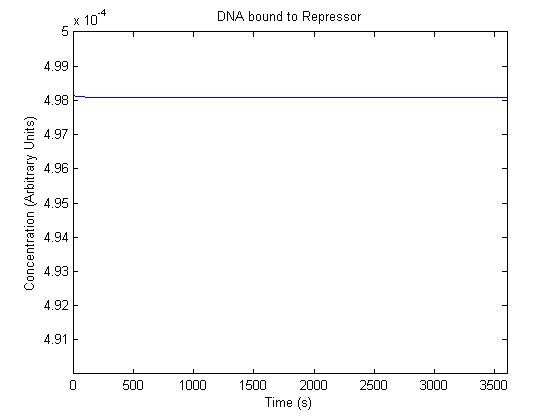
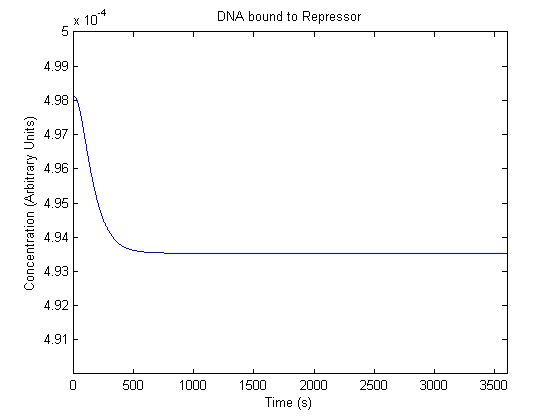
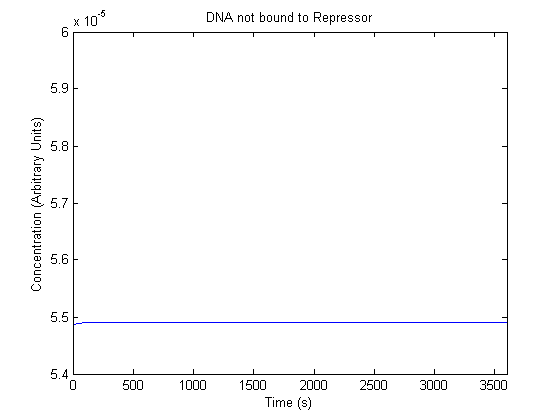
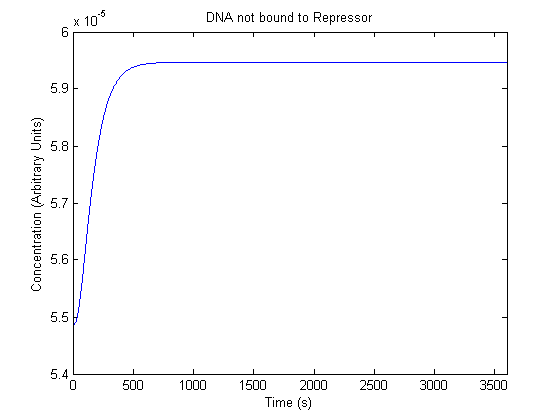
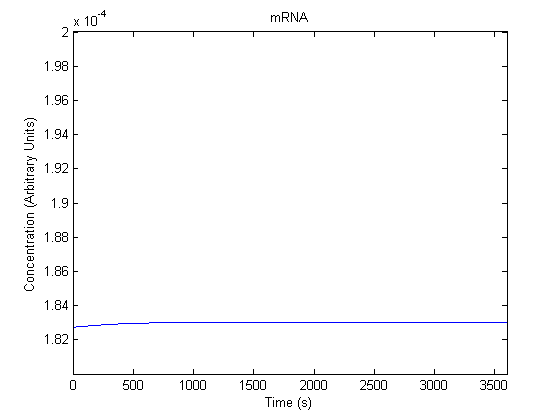
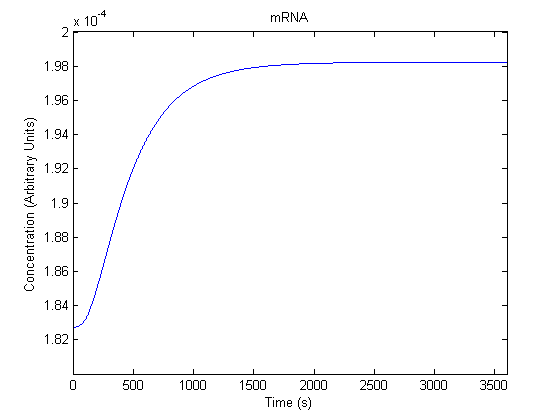
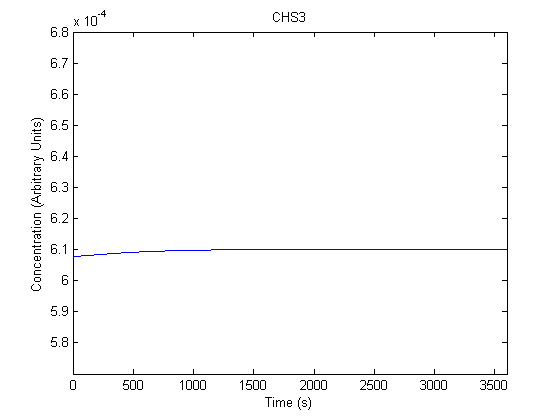
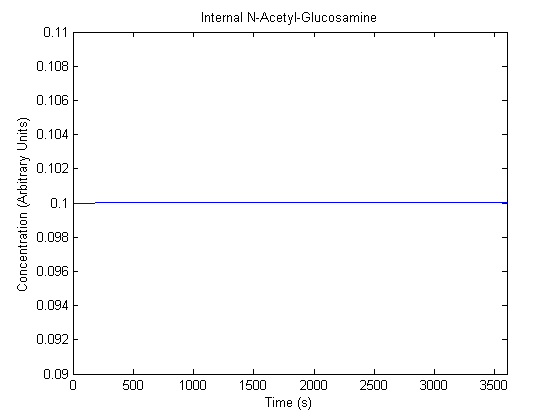
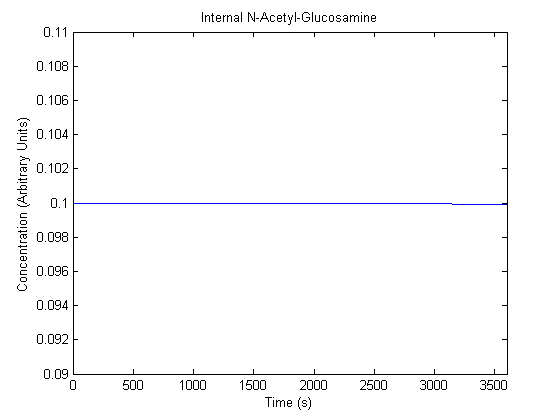
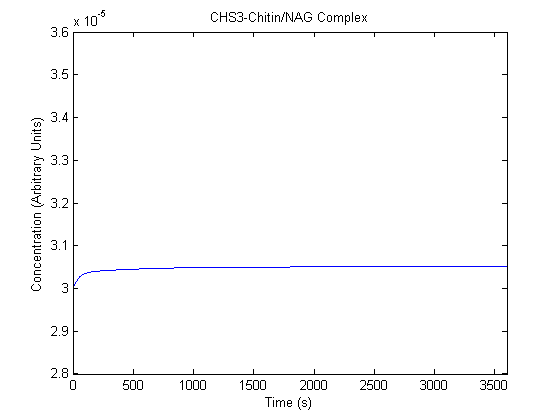
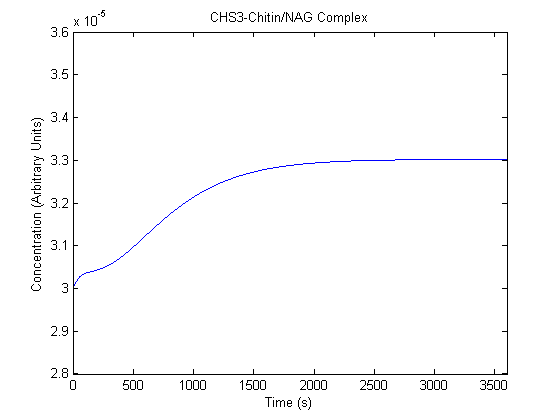
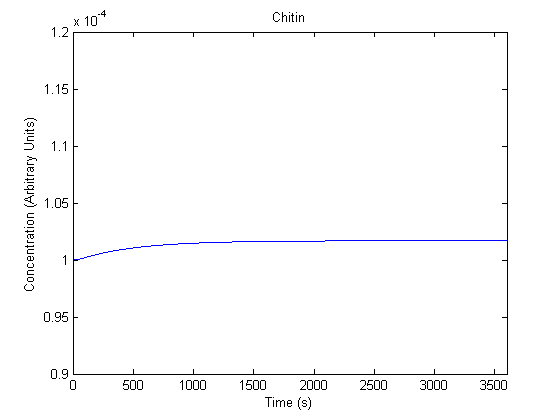
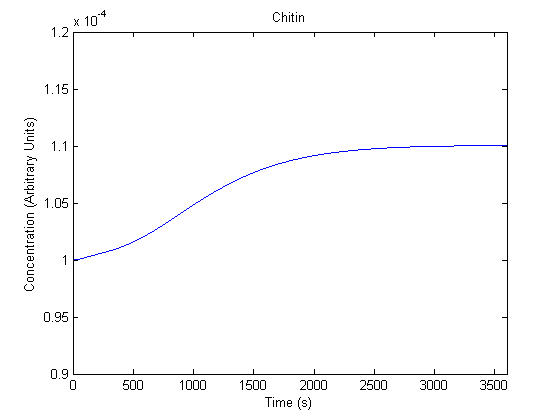
IPTG DiffusionFirst, Fick's Law of Diffusion was modeled through MATLAB. The diffusion constant used was 220um^2/s.[4] IPTG was sprayed at the top of the colony, which then diffuses as according to Fick's law. The spatially different local IPTG concentration will then differentially induce downstream processes. This distinction was necessary in our project in order to establish a Chitin layer on the top of the biofilm. Semi-Empirical Variable/Constant DeterminationStatus: Under Development The initial plan was to use lacI-constitutive expression / lac-operon (CP-LacpI) part with Green Fluorescent Protein to acquire empirical data. By testing various combinations of CP/LacpI, RBS, and IPTG concentrations, the acquisition of a broad range of expression level (GFP fluorescence) over time could be acquired through a plate reader. This data would be used to determine many of the rate constants as well as initial concentration values, thus generating a more accurate semi-empirical kinetics model. However, at the time of the wiki-freeze, data acquisition is incomplete. Current ModelThe plots of the non-induced and the induced system are as follows:
Future ConcernsOverall, the model, though logical, is not yet fit for application, mostly due to the lack of empirical data to which the model could be fit and/or tested. Once fit, the rate constant values and initial concentration values will be much more accurate. The following concerns deal primarily with problems that could possibly not be corrected even with empirical data.
Future WorkAside from being generally accurate, the model should perform the following functions:
References1. A novel structured kinetic modeling approach for the analysis of plasmid instability in recombinant bacterial cultures William E. Bentley, Dhinakar S. Kompala Article first published online: 18 FEB 2004 DOI: 10.1002/bit.260330108 http://onlinelibrary.wiley.com/doi/10.1002/bit.260330108/pdf
Jongdae Lee, W. Fred Ramirez Article first published online: 19 FEB 2004 DOI: 10.1002/bit.260390608 http://onlinelibrary.wiley.com/doi/10.1002/bit.260390608/pdf
DOMINIQUE MENGIN-LECREULX, BERNARD FLOURET, AND JEAN VAN HEIJENOORT* E.R. 245 du C.N.R.S., Institut de Biochimie, Universit' Paris-Sud, Orsay, 91405, France Received 9 February 1983/Accepted 15 March 1983 http://www.ncbi.nlm.nih.gov/pmc/articles/PMC217602/pdf/jbacter00247-0262.pdf
Philip S. Stewart Center for Biofilm Engineering and Department of Chemical Engineering, Montana State University–Bozeman, Bozeman, Montana, 59717-3980 http://www.ncbi.nlm.nih.gov/pmc/articles/PMC148055/pdf/0965.pdf
PATRICIA L. EDELMANN' AND GORDON EDLIN Department of Genetics, University of California, Davis, California 95616 Received for publication 21 March 1974 http://www.ncbi.nlm.nih.gov/pmc/articles/PMC245824/pdf/jbacter00335-0105.pdf
MATLAB m-file%IPTG PREDETERMINATION %finite difference method %diffusion equation (Fick's 2nd Law) %c=c0*(erfc*x/sqrt(2*D*t)) %D*(Ci+1-2C+Ci-1)/dx^2 = Ci/dt %x goes from 0 (top) to 100 micrometers %D=IPTG is a modified monosaccharide, so we can estimate from Table 1 that %its diffusion coefficient in water at 25°C will be ca. 6.5 × 10?6 cm2 s?1. %Scaling to 37°C and taking De/Daq to be 0.25, De is found to be 2.2 × 10?6 cm2 s?1 %http://www.ncbi.nlm.nih.gov/pmc/articles/PMC148055/ %% clear clc %INITIALIZE D=220; %um^2/s c0=14.298; %mg so 3ml spray of 20mM iptg %in comparison 23.83mg of iptg is in 5ml 20mM dx=1; %um xmax=100; %um; 100um total dt=.002; %s tmax=10; %s; 1 hour total C=zeros(xmax/dx,tmax/dt); %rows = same time %also, (x,t) x is row, t is column C_Rate=zeros(xmax/dt,1); C(1,1)=c0; %Time Step for t=1:1:tmax/dt-1; %s for x=1:1:(xmax/dx) %um if x==1%account for x=1 boundary condition C_Rate(x)=D*(C(x+1,t)-C(x,t))/(dx^2); elseif x==xmax/dx %account for x=xmax boundary condition C_Rate(x)=D*(C(x-1,t)-C(x,t))/(dx^2); else%BULK C_Rate(x)=D*(C(x-1,t)+C(x+1,t)-2*C(x,t))/(dx^2); end C(x,t+1)=C(x,t)+C_Rate(x)*dt; end t*.002 end %% %Compile into 1s parts %newC=zeros(100,tmax/dt/500); counts=1; for t=1:500:tmax/dt-1 %.002*x=1; newC(:,counts)=C(:,t); counts=counts+1; end %% %visualize newC for t=1:1:tmax/dt/500 XX=0:dx:xmax-dx; YY=newC(:,t); plot(XX,YY,'k.'); axis([0 100 0 2]) text(50,1.8,sprintf('Time is: %g s', t*dt)); text(50,1.7,sprintf('IPTG Mass balance is: %g mg', sum(C(:,t)))); xlabel('Distance from surface (um)') ylabel('IPTG (mg)') Mov(t)=getframe(); %pause(1); end %% %VISUALIZE blah=1; for t=1:7:tmax/dt XX=xmax-dx-100:-dx:0-100; YY=C(:,t); plot(YY,XX,'k.'); axis([0 2 -100 0]) text(1.2,-30,sprintf('Time: %g s', t*dt)); %text(50,1.7,sprintf('IPTG Mass balance is: %g mg', sum(C(:,t)))); ylabel('Distance from surface (um)') xlabel('IPTG (mg)') VID(blah)=getframe(gcf); blah=blah+1; end % Updated kinetics model %{ Iex - external inducer or iptg Iin - internal inducer or iptg Ii - lac inhibitor / iptg complex i - lac inhibitor Db - DNA bound to inhibitor Dunb - DNA not bound to inhibitor R - mRNA E - Enzyme Chitin Synthase So - External Substrate - N-Acetyl Glucosamine Si - Internal Substrate - N-Acetyl Glucosamine CC - Enzyme Substrate Complex P - Protein - Chitin %} dt=1; tmax=3600; dx=1; xmax=100; %General Array Structure: (Depth (um), Time (s)) %Depth = 0-100 micrometers %Time = 0- 3600 seconds preset=zeros(xmax,tmax); Iin=preset;Ii=preset;i=preset;Db=preset;Dunb=preset;Re=preset;E=preset;Si=preset;CC=preset;P=preset; %initial concentration a=load('newC.mat'); %Iex is diff - assume cell intake << exist Iex=zeros(100,3600);%a.newC();% Iin(:,1)=0; %initially IPTG inside the cell is 0 Ii(:,1)=0; %no iptg, no Ii i(:,1)=0.9973*10^-4; %10^-7 to 10^-8 M which is 10^-4 to 10^5 mM http://www.ncbi.nlm.nih.gov/pmc/articles/PMC245824/pdf/jbacter00335-0105.pdf %DNA - partsregistry - 200 copy number - 200/(6.23*10^-23)/(6*10^-16 %volume)*1000 = 5.53*10^-4mM dper=0.9008; Db(:,1)=5.53*dper*10^-4; %say 90% is bound no idea Dunb(:,1)=5.53*(1-dper)*10^-4; %say 10% unbound no idea Re(:,1)=1.82735*10^-4; %initially, no RNA E(:,1)=6.08*10^-4; %initially no enzyme So=33.9; %1 pill per plate ~ 750mg/100ml /221.21g/mol /1000*1000*1000 is 33.9mM Si(:,1)=10^-1; %http://www.ncbi.nlm.nih.gov/pmc/articles/PMC217602/pdf/jbacter00247-0262.pdf CC(:,1)=3*10^-5; %initially 0 P(:,1)=1*10^-4; %initially 0 %rate constants kIin=.05;%safe to say diffuses within minutes kIex=.05;%permeability must be similar kIif=.01; kIir=.01; kDbf=100; kDbr=.0011; ktscribe=.01; ktslate=.01; kRdeg=.003; kEdeg=.003; kPdeg=.003; ksin=0.000000009; kCf=.01; kCr=.01; kP=.01; %Begin Loop %FILL IN THE BLANKS %General Array Structure: (Depth (um), Time (s)) for tt=1:1:tmax/dt-1 for xx=1:1:xmax/dx %Predetermine diffusion %dIex=DIF(xx,tt) + kIin*Iin(xx,tt) - kIex*Iex(xx,tt); dIin=kIin*Iex(xx,tt) -kIex*Iin(xx,tt) +kIir*Ii(xx,tt) -kIif*Iin(xx,tt)*i(xx,tt); dIi=kIif*Iin(xx,tt)*i(xx,tt) -kIir*Ii(xx,tt); di=kIir*Ii(xx,tt) -kIif*Iin(xx,tt)*i(xx,tt) +kDbr*Db(xx,tt) -kDbf*i(xx,tt)*Dunb(xx,tt); dDb=kDbf*i(xx,tt)*Dunb(xx,tt) -kDbr*Db(xx,tt); dDunb=kDbr*Db(xx,tt) -kDbf*i(xx,tt)*Dunb(xx,tt); dRe=ktscribe*Dunb(xx,tt) -kRdeg*Re(xx,tt); dE=ktslate*Re(xx,tt) -kEdeg*E(xx,tt) +kCr*CC(xx,tt) +kP*CC(xx,tt) -kCf*E(xx,tt)*Si(xx,tt); dSi=ksin*So -kCf*E(xx,tt)*Si(xx,tt) +kCr*CC(xx,tt); dCC=kCf*E(xx,tt)*Si(xx,tt) -kCr*CC(xx,tt) - kP*CC(xx,tt); dP=kP*CC(xx,tt) -kPdeg*P(xx,tt); %Iex(xx,tt+1)=Iex(xx,tt)+dIex*dt; Iin(xx,tt+1)=Iin(xx,tt)+dIin*dt; Ii(xx,tt+1)=Ii(xx,tt)+dIi*dt; i(xx,tt+1)=i(xx,tt)+di*dt; Db(xx,tt+1)=Db(xx,tt)+dDb*dt; Dunb(xx,tt+1)=Dunb(xx,tt)+dDunb*dt; Re(xx,tt+1)=Re(xx,tt)+dRe*dt; E(xx,tt+1)=E(xx,tt)+dE*dt; Si(xx,tt+1)=Si(xx,tt)+dSi*dt; CC(xx,tt+1)=CC(xx,tt)+dCC*dt; P(xx,tt+1)=P(xx,tt)+dP*dt; end tt*dt/tmax*100 end | ||||||||||||||||||||||||||||||||||||
 "
"