Team:Northwestern/Project/Modeling
From 2010.igem.org
(→Introduction / Objective) |
(→Modeling) |
||
| Line 165: | Line 165: | ||
In terms of our iGEM project, this model was employed to explore the effect of IPTG concentration and diffusion, lacI concentration (determined by the combination part of constitutive promoter, ribosome binding site, lacI gene, double terminator, lac promoter/operon), and the ribosome binding site (of the final product-producing enzyme) on the concentrations of all species involved - described in the following sections - and especially on Chitin Synthase and Chitin concentration and the corresponding rates. | In terms of our iGEM project, this model was employed to explore the effect of IPTG concentration and diffusion, lacI concentration (determined by the combination part of constitutive promoter, ribosome binding site, lacI gene, double terminator, lac promoter/operon), and the ribosome binding site (of the final product-producing enzyme) on the concentrations of all species involved - described in the following sections - and especially on Chitin Synthase and Chitin concentration and the corresponding rates. | ||
| - | ==''' | + | =='''Model Development'''== |
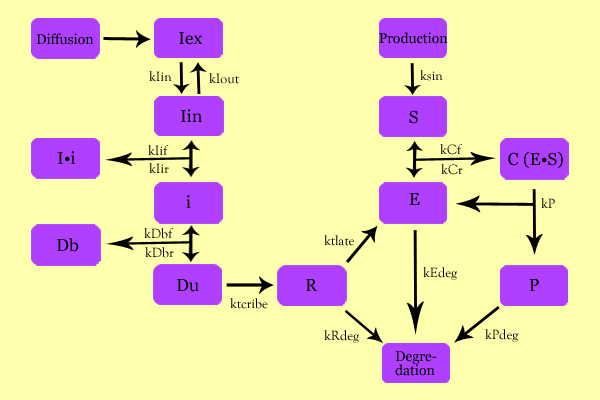
| - | + | The following schematic summarizes the mathematical model we formulated to describe our system. | |
| - | + | ||
| - | + | ||
[[Image:SuperModeling.jpg|600px|center]] | [[Image:SuperModeling.jpg|600px|center]] | ||
| Line 187: | Line 185: | ||
* C: Enzyme Substrate Complex (CHS3-(N-Acetyl-Glucosamine)-Chitin or (NAG)n Complex) | * C: Enzyme Substrate Complex (CHS3-(N-Acetyl-Glucosamine)-Chitin or (NAG)n Complex) | ||
* P: Protein Product (Chitin or (NAG)n+1) | * P: Protein Product (Chitin or (NAG)n+1) | ||
| + | |||
| + | |||
| + | ==='''Constants'''=== | ||
| + | |||
| + | Rate Constants: | ||
| + | |||
| + | * kIin - Inducer diffusion into cell from surrounding environment | ||
| + | * kIout - Inducer diffusion out of cell to surrounding environment | ||
| + | * kIif - Inducer and Repressor binding to form Inducer-Repressor Complex | ||
| + | * kIir - Inducer-Repressor Complex unbinding to form Inducer and Repressor | ||
| + | * kDbf - Repressor binding to DNA to form DNA-Repressor Complex | ||
| + | * kDbr - DNA-Repressor Complex unbinding to form free unbound DNA | ||
| + | * ktcribe - transcription | ||
| + | * ktlate - translation | ||
| + | * ksin - endogenous substrate production | ||
| + | * kCf - Substrate-Enzyme Complex Formation | ||
| + | * kCr - Substrate-Enzyme Complex unbinding to form Substrate and Enzyme | ||
| + | * kP - Substrate-Enzyme Complex forming Product and Enzyme | ||
| + | * kEdeg - Enzyme Degredation | ||
| + | * kRdeg - RNA Degredation | ||
| + | * kPdeg - Protein Degredation | ||
| Line 193: | Line 212: | ||
The differential of the variables were found as follows: | The differential of the variables were found as follows: | ||
| - | * dIin = kIin*Iex - kIex*Iin + kIir*Ii - kIif*Iin*i | + | * dIin/dt = kIin*Iex - kIex*Iin + kIir*Ii - kIif*Iin*i |
| - | * dIi = kIif*Iin*i - kIir*Ii | + | * dIi/dt = kIif*Iin*i - kIir*Ii |
| - | * di = kIir*Ii - kIif*Iin*i + kDbr*Db - kDbf*i*Dunb | + | * di/dt = kIir*Ii - kIif*Iin*i + kDbr*Db - kDbf*i*Dunb |
| - | * dDb = kDbf*i*Dunb - kDbr*Db | + | * dDb/dt = kDbf*i*Dunb - kDbr*Db |
| - | * dDunb = kDbr*Db - kDbf*i*Dunb | + | * dDunb/dt = kDbr*Db - kDbf*i*Dunb |
| - | * dRe = ktscribe*Dunb - kRdeg*Re | + | * dRe/dt = ktscribe*Dunb - kRdeg*Re |
| - | * dE = ktslate*Re - kEdeg*E + kCr*CC + kP*CC - kCf*E*Si | + | * dE/dt = ktslate*Re - kEdeg*E + kCr*CC + kP*CC - kCf*E*Si |
| - | * dSi = ksin*So - kCf*E*Si + kCr*CC | + | * dSi/dt = ksin*So - kCf*E*Si + kCr*CC |
| - | * dCC = kCf*E*Si - kCr*CC - kP*CC | + | * dCC/dt = kCf*E*Si - kCr*CC - kP*CC |
| - | * dP = kP*CC - kPdeg*P | + | * dP/dt = kP*CC - kPdeg*P |
| - | ===''' | + | ==='''Assumptions'''=== |
| - | + | In order to determine the initial or steady state concentrations of the involved species and to determine the rate constants, the following assumptions were made: | |
| - | |||
| - | IPTG | + | ===='''IPTG Diffusion'''==== |
| - | The | + | First, Fick's Law of Diffusion was modeled through MATLAB. The diffusion constant used was 220um^2/s.[4] |
| - | + | It was assumed that IPTG was not consumed nor degraded | |
| - | + | We also assumed that IPTG uptake was minor was compared to the concentration in the biofilm, and so that the external IPTG was determined solely by Fick's Law, not by internalization. | |
| - | |||
| - | + | ===='''Constant Determination'''==== | |
| - | + | Initially, the following initial concentration values were assumed: | |
| - | + | * Iex: Described in the previous section | |
| + | * Iin: Internal IPTG initially assumed to be 0 | ||
| + | * Ii: 0, because no IPTG means IPTG-repressor complex | ||
| + | * i: Value acquired from [5] as between 10^-5 and 10^-4 and adjusted to 9.973*10^-5 | ||
| + | * Db: Calculated, knowing the expression vector is a 200 copy number plasmid; of the DNA, approximated that 90.08% is bound | ||
| + | * Dunb: Calculated, knowing the expression vector is a 200 copy number plasmid; of the DNA, approximated that 9.92% is bound | ||
| + | * Re: Determined to be 1.82735*10^-4 by achieving steady state with the model | ||
| + | * E: Determined to be 6.08*10^-4 by achieving steady state with the model | ||
| + | * So: External Substrate calculated by using amount added in enriched media as 33.9 | ||
| + | * Si: Determined from [3] to be 10^-1 | ||
| + | * C: Determined to be 3*10^-5by achieving steady state with the model | ||
| + | * P: Determined to be 1*10^-4 by achieving steady state with the model | ||
| - | + | The rate constant values were assumed to be the following: | |
| - | + | * kIin: .05 yielded reasonable diffusion times | |
| + | * kIex: .05 since simple diffusion, the internal rate constant must be similar if not identical to the external rate constant | ||
| + | * kIif: .01 yielded reasonable repressor/Inducer interactions | ||
| + | * kIir: .01 yielded reasonable repressor/Inducer interactions | ||
| + | * kDbf: 100 yielded reasonable DNA/repressor interactions | ||
| + | * kDbr: .0011 yielded reasonable DNA/repressor interactions | ||
| + | * ktscribe: .01 yielded reasonable production levels | ||
| + | * ktslate: .01 yielded reasonable production levels | ||
| + | * kRdeg: .003 yielded reasonable degredation | ||
| + | * kEdeg: .003 yielded reasonable degredation | ||
| + | * kPdeg: .003 yielded reasonable degredation | ||
| + | * ksin: 0.000000009 yielded reasonable internalization of substrate | ||
| + | * kCf: .01 yielded reasonable production levels | ||
| + | * kCr: .01 yielded reasonable production levels | ||
| + | * kP: .01 yielded reasonable production levels | ||
| + | |||
| + | |||
| + | =='''Results'''== | ||
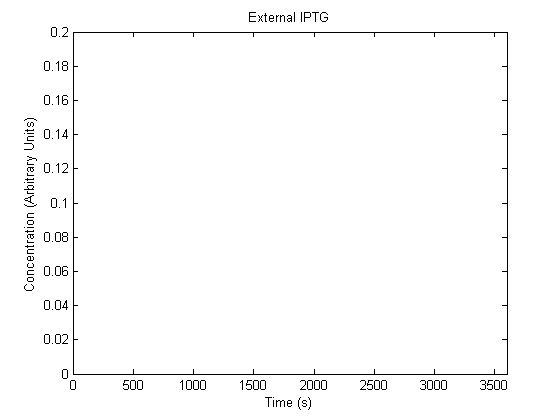
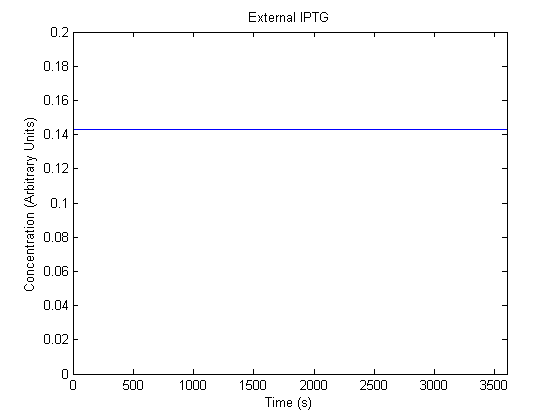
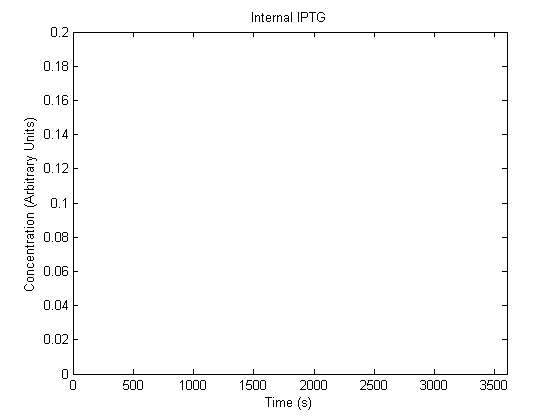
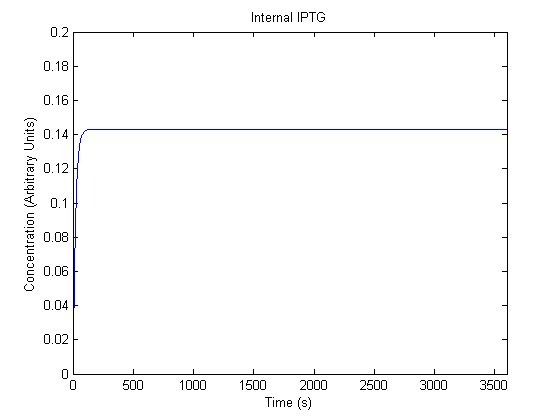
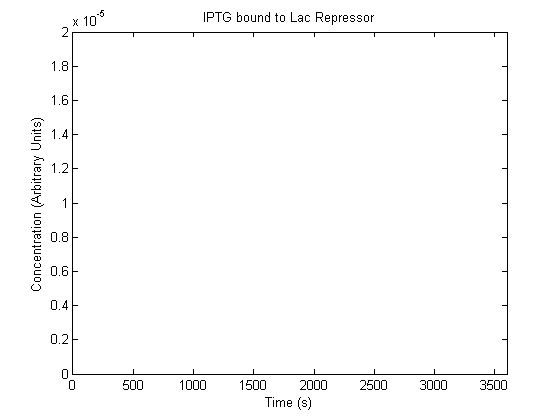
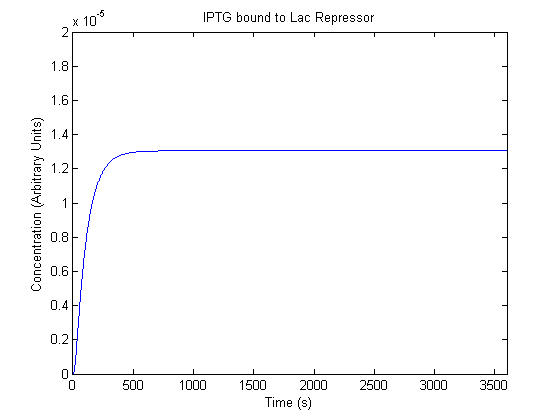
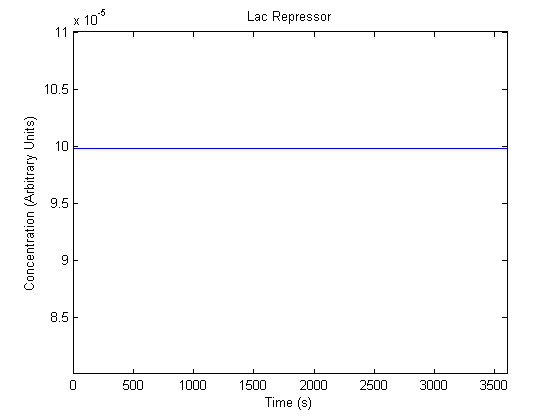
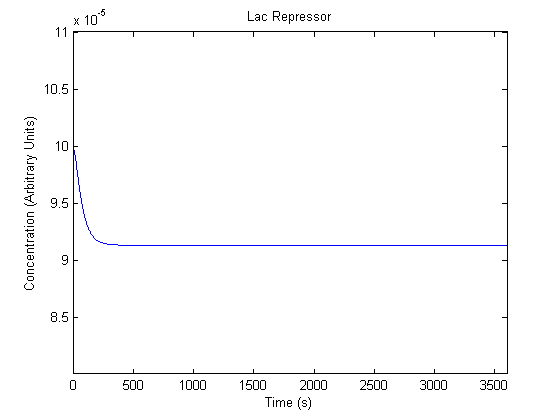
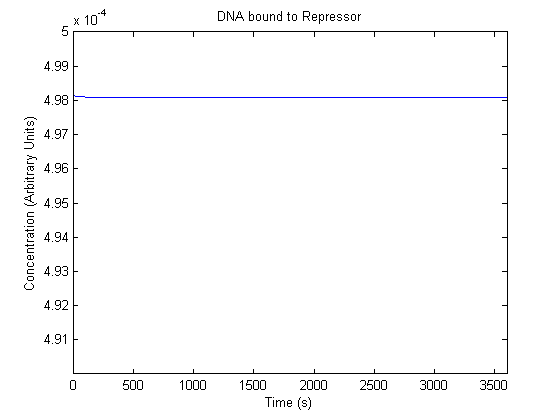
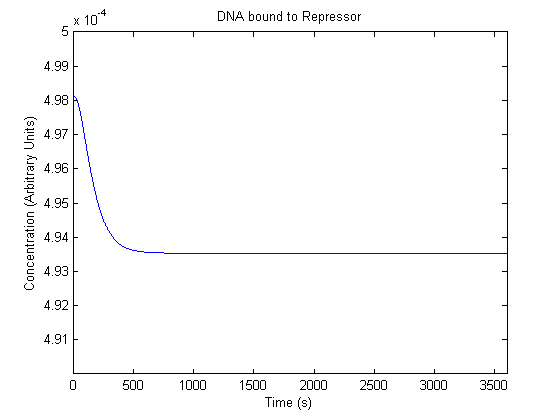
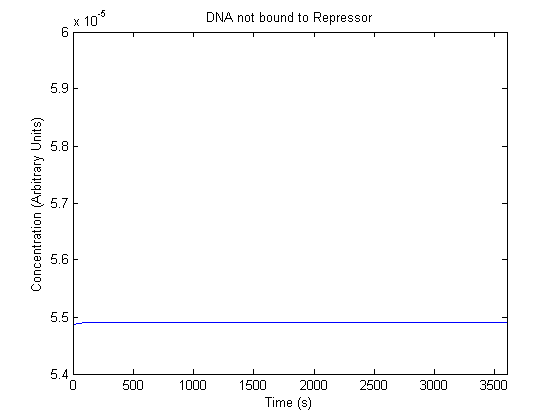
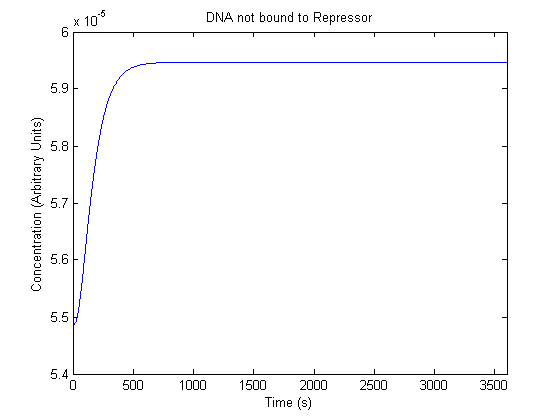
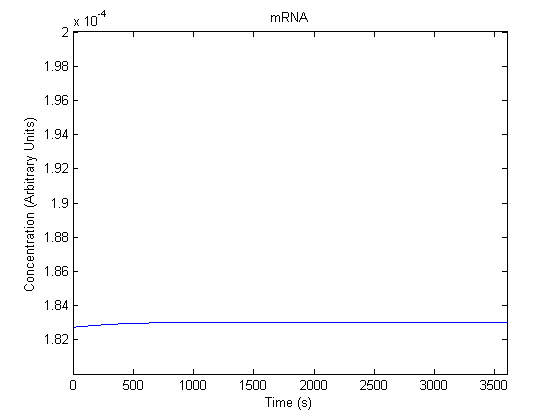
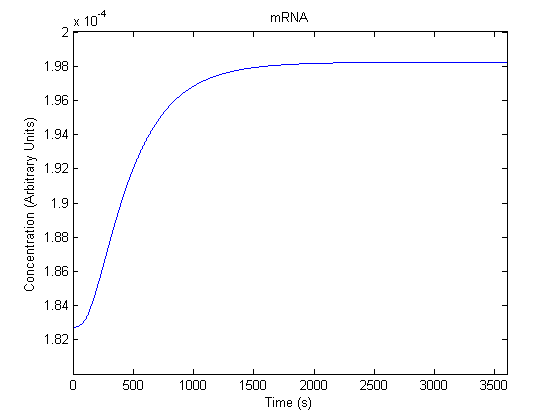
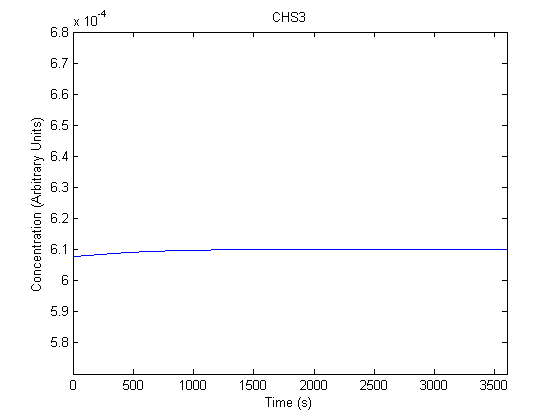
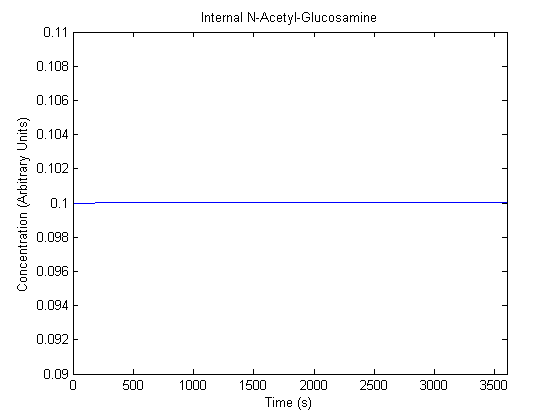
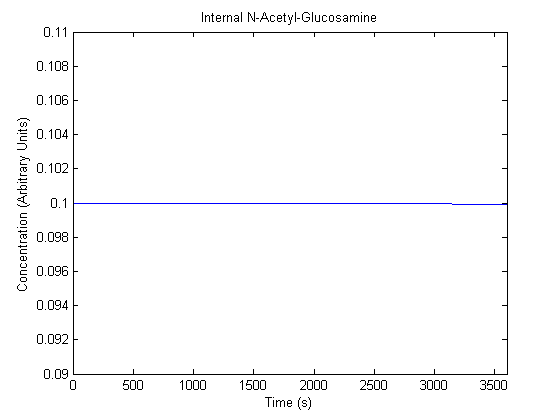
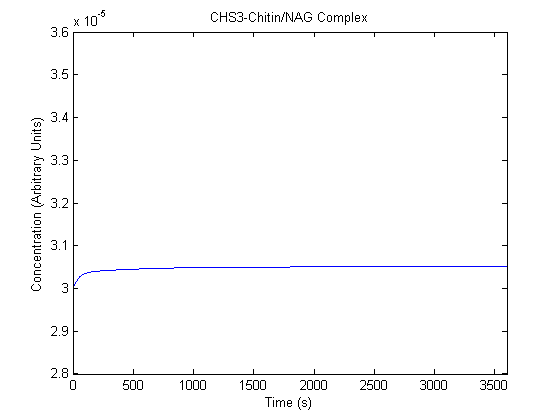
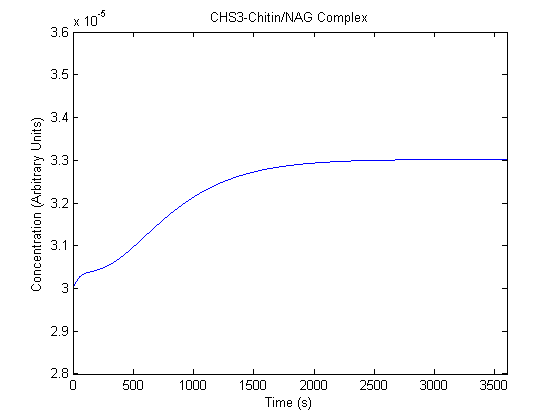
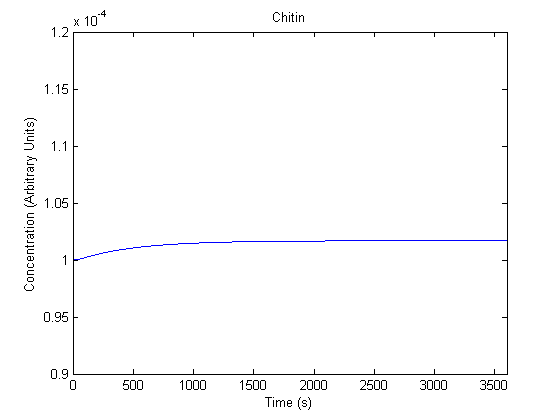
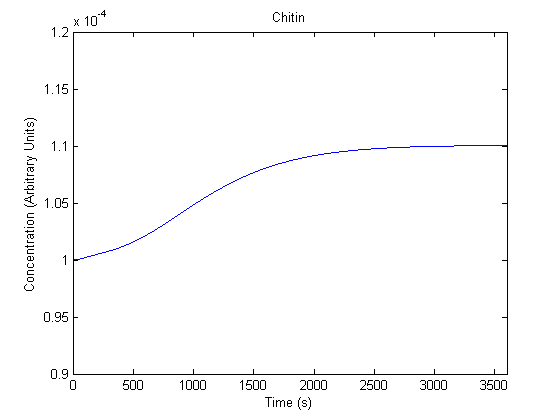
The plots of the non-induced and the induced system are as follows: | The plots of the non-induced and the induced system are as follows: | ||
| Line 281: | Line 326: | ||
*Differentiate protein production between expression vectors with different Copy Number Plasmids. | *Differentiate protein production between expression vectors with different Copy Number Plasmids. | ||
| + | |||
| + | [[Image:loopydoops.gif]] | ||
=='''References'''== | =='''References'''== | ||
Revision as of 01:42, 28 October 2010
| Home | Brainstorm | Team | Acknowledgements | Project | Human Practices | Parts | Notebook | Calendar | Protocol | Safety | Links | References | Media | Contact |
|---|
|
| ||||||||||||||||||||||||||||||||||||
Introduction / ObjectiveWe constructed a mathematical model to explore and characterize the operation as well as the modulation of our experimental system. In particular, we wanted to investigate the effect of varying parameters that we could experimentally modulate on the system. Those parameters include:
Model DevelopmentThe following schematic summarizes the mathematical model we formulated to describe our system.
Variables
ConstantsRate Constants:
EquationsThe differential of the variables were found as follows:
AssumptionsIn order to determine the initial or steady state concentrations of the involved species and to determine the rate constants, the following assumptions were made:
IPTG DiffusionFirst, Fick's Law of Diffusion was modeled through MATLAB. The diffusion constant used was 220um^2/s.[4] It was assumed that IPTG was not consumed nor degraded We also assumed that IPTG uptake was minor was compared to the concentration in the biofilm, and so that the external IPTG was determined solely by Fick's Law, not by internalization.
Constant DeterminationInitially, the following initial concentration values were assumed:
The rate constant values were assumed to be the following:
ResultsThe plots of the non-induced and the induced system are as follows:
Future ConcernsOverall, the model, though logical, is not yet fit for application, partially due to the lack of empirical data to which the model could be fit and/or tested. Once fit, the rate constant values and initial concentration values will be much more accurate. The following concerns deal primarily with problems that could possibly not be corrected even with empirical data.
Future WorkAside from being generally accurate, the model should perform the following functions:
References1. A novel structured kinetic modeling approach for the analysis of plasmid instability in recombinant bacterial cultures William E. Bentley, Dhinakar S. Kompala Article first published online: 18 FEB 2004 DOI: 10.1002/bit.260330108 http://onlinelibrary.wiley.com/doi/10.1002/bit.260330108/pdf
Jongdae Lee, W. Fred Ramirez Article first published online: 19 FEB 2004 DOI: 10.1002/bit.260390608 http://onlinelibrary.wiley.com/doi/10.1002/bit.260390608/pdf
DOMINIQUE MENGIN-LECREULX, BERNARD FLOURET, AND JEAN VAN HEIJENOORT* E.R. 245 du C.N.R.S., Institut de Biochimie, Universit' Paris-Sud, Orsay, 91405, France Received 9 February 1983/Accepted 15 March 1983 http://www.ncbi.nlm.nih.gov/pmc/articles/PMC217602/pdf/jbacter00247-0262.pdf
Philip S. Stewart Center for Biofilm Engineering and Department of Chemical Engineering, Montana State University–Bozeman, Bozeman, Montana, 59717-3980 http://www.ncbi.nlm.nih.gov/pmc/articles/PMC148055/pdf/0965.pdf
PATRICIA L. EDELMANN' AND GORDON EDLIN Department of Genetics, University of California, Davis, California 95616 Received for publication 21 March 1974 http://www.ncbi.nlm.nih.gov/pmc/articles/PMC245824/pdf/jbacter00335-0105.pdf
MATLAB m-file%IPTG PREDETERMINATION %finite difference method %diffusion equation (Fick's 2nd Law) %c=c0*(erfc*x/sqrt(2*D*t)) %D*(Ci+1-2C+Ci-1)/dx^2 = Ci/dt %x goes from 0 (top) to 100 micrometers %D=IPTG is a modified monosaccharide, so we can estimate from Table 1 that %its diffusion coefficient in water at 25°C will be ca. 6.5 × 10?6 cm2 s?1. %Scaling to 37°C and taking De/Daq to be 0.25, De is found to be 2.2 × 10?6 cm2 s?1 %http://www.ncbi.nlm.nih.gov/pmc/articles/PMC148055/ %% clear clc %INITIALIZE D=220; %um^2/s c0=14.298; %mg so 3ml spray of 20mM iptg %in comparison 23.83mg of iptg is in 5ml 20mM dx=1; %um xmax=100; %um; 100um total dt=.002; %s tmax=10; %s; 1 hour total C=zeros(xmax/dx,tmax/dt); %rows = same time %also, (x,t) x is row, t is column C_Rate=zeros(xmax/dt,1); C(1,1)=c0; %Time Step for t=1:1:tmax/dt-1; %s for x=1:1:(xmax/dx) %um if x==1%account for x=1 boundary condition C_Rate(x)=D*(C(x+1,t)-C(x,t))/(dx^2); elseif x==xmax/dx %account for x=xmax boundary condition C_Rate(x)=D*(C(x-1,t)-C(x,t))/(dx^2); else%BULK C_Rate(x)=D*(C(x-1,t)+C(x+1,t)-2*C(x,t))/(dx^2); end C(x,t+1)=C(x,t)+C_Rate(x)*dt; end t*.002 end %% %Compile into 1s parts %newC=zeros(100,tmax/dt/500); counts=1; for t=1:500:tmax/dt-1 %.002*x=1; newC(:,counts)=C(:,t); counts=counts+1; end %% %visualize newC for t=1:1:tmax/dt/500 XX=0:dx:xmax-dx; YY=newC(:,t); plot(XX,YY,'k.'); axis([0 100 0 2]) text(50,1.8,sprintf('Time is: %g s', t*dt)); text(50,1.7,sprintf('IPTG Mass balance is: %g mg', sum(C(:,t)))); xlabel('Distance from surface (um)') ylabel('IPTG (mg)') Mov(t)=getframe(); %pause(1); end %% %VISUALIZE blah=1; for t=1:7:tmax/dt XX=xmax-dx-100:-dx:0-100; YY=C(:,t); plot(YY,XX,'k.'); axis([0 2 -100 0]) text(1.2,-30,sprintf('Time: %g s', t*dt)); %text(50,1.7,sprintf('IPTG Mass balance is: %g mg', sum(C(:,t)))); ylabel('Distance from surface (um)') xlabel('IPTG (mg)') VID(blah)=getframe(gcf); blah=blah+1; end % Updated kinetics model %{ Iex - external inducer or iptg Iin - internal inducer or iptg Ii - lac inhibitor / iptg complex i - lac inhibitor Db - DNA bound to inhibitor Dunb - DNA not bound to inhibitor R - mRNA E - Enzyme Chitin Synthase So - External Substrate - N-Acetyl Glucosamine Si - Internal Substrate - N-Acetyl Glucosamine CC - Enzyme Substrate Complex P - Protein - Chitin %} dt=1; tmax=3600; dx=1; xmax=100; %General Array Structure: (Depth (um), Time (s)) %Depth = 0-100 micrometers %Time = 0- 3600 seconds preset=zeros(xmax,tmax); Iin=preset;Ii=preset;i=preset;Db=preset;Dunb=preset;Re=preset;E=preset;Si=preset;CC=preset;P=preset; %initial concentration a=load('newC.mat'); %Iex is diff - assume cell intake << exist Iex=zeros(100,3600);%a.newC();% Iin(:,1)=0; %initially IPTG inside the cell is 0 Ii(:,1)=0; %no iptg, no Ii i(:,1)=0.9973*10^-4; %10^-7 to 10^-8 M which is 10^-4 to 10^5 mM http://www.ncbi.nlm.nih.gov/pmc/articles/PMC245824/pdf/jbacter00335-0105.pdf %DNA - partsregistry - 200 copy number - 200/(6.23*10^-23)/(6*10^-16 %volume)*1000 = 5.53*10^-4mM dper=0.9008; Db(:,1)=5.53*dper*10^-4; %say 90% is bound no idea Dunb(:,1)=5.53*(1-dper)*10^-4; %say 10% unbound no idea Re(:,1)=1.82735*10^-4; %initially, no RNA E(:,1)=6.08*10^-4; %initially no enzyme So=33.9; %1 pill per plate ~ 750mg/100ml /221.21g/mol /1000*1000*1000 is 33.9mM Si(:,1)=10^-1; %http://www.ncbi.nlm.nih.gov/pmc/articles/PMC217602/pdf/jbacter00247-0262.pdf CC(:,1)=3*10^-5; %initially 0 P(:,1)=1*10^-4; %initially 0 %rate constants kIin=.05;%safe to say diffuses within minutes kIex=.05;%permeability must be similar kIif=.01; kIir=.01; kDbf=100; kDbr=.0011; ktscribe=.01; ktslate=.01; kRdeg=.003; kEdeg=.003; kPdeg=.003; ksin=0.000000009; kCf=.01; kCr=.01; kP=.01; %Begin Loop %FILL IN THE BLANKS %General Array Structure: (Depth (um), Time (s)) for tt=1:1:tmax/dt-1 for xx=1:1:xmax/dx %Predetermine diffusion %dIex=DIF(xx,tt) + kIin*Iin(xx,tt) - kIex*Iex(xx,tt); dIin=kIin*Iex(xx,tt) -kIex*Iin(xx,tt) +kIir*Ii(xx,tt) -kIif*Iin(xx,tt)*i(xx,tt); dIi=kIif*Iin(xx,tt)*i(xx,tt) -kIir*Ii(xx,tt); di=kIir*Ii(xx,tt) -kIif*Iin(xx,tt)*i(xx,tt) +kDbr*Db(xx,tt) -kDbf*i(xx,tt)*Dunb(xx,tt); dDb=kDbf*i(xx,tt)*Dunb(xx,tt) -kDbr*Db(xx,tt); dDunb=kDbr*Db(xx,tt) -kDbf*i(xx,tt)*Dunb(xx,tt); dRe=ktscribe*Dunb(xx,tt) -kRdeg*Re(xx,tt); dE=ktslate*Re(xx,tt) -kEdeg*E(xx,tt) +kCr*CC(xx,tt) +kP*CC(xx,tt) -kCf*E(xx,tt)*Si(xx,tt); dSi=ksin*So -kCf*E(xx,tt)*Si(xx,tt) +kCr*CC(xx,tt); dCC=kCf*E(xx,tt)*Si(xx,tt) -kCr*CC(xx,tt) - kP*CC(xx,tt); dP=kP*CC(xx,tt) -kPdeg*P(xx,tt); %Iex(xx,tt+1)=Iex(xx,tt)+dIex*dt; Iin(xx,tt+1)=Iin(xx,tt)+dIin*dt; Ii(xx,tt+1)=Ii(xx,tt)+dIi*dt; i(xx,tt+1)=i(xx,tt)+di*dt; Db(xx,tt+1)=Db(xx,tt)+dDb*dt; Dunb(xx,tt+1)=Dunb(xx,tt)+dDunb*dt; Re(xx,tt+1)=Re(xx,tt)+dRe*dt; E(xx,tt+1)=E(xx,tt)+dE*dt; Si(xx,tt+1)=Si(xx,tt)+dSi*dt; CC(xx,tt+1)=CC(xx,tt)+dCC*dt; P(xx,tt+1)=P(xx,tt)+dP*dt; end tt*dt/tmax*100 end | ||||||||||||||||||||||||||||||||||||
 "
"