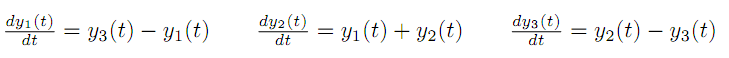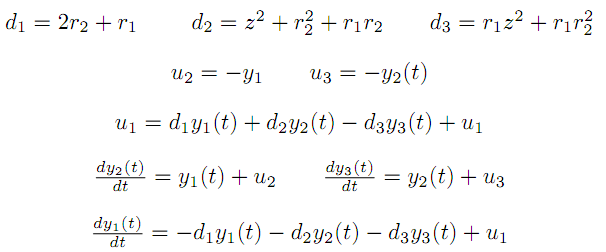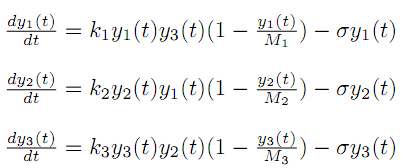Team:Mexico-UNAM-CINVESTAV/Human Practices/Collaboration
From 2010.igem.org
m (first draft of colaboration) |
m |
||
| (10 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{Mexico-UNAM-CINVESTAV-HEADER}} | {{Mexico-UNAM-CINVESTAV-HEADER}} | ||
| + | __NOTOC__ | ||
| + | ==Participation in other surveys== | ||
This year we think was the most collaborative one. there were plenty of surveys, meetings and intense information exchange. | This year we think was the most collaborative one. there were plenty of surveys, meetings and intense information exchange. | ||
| Line 12: | Line 14: | ||
We also made a contribution to the UNAM Genomics Team modeling, by proposing a mathematical model of their three component positive feedback network. | We also made a contribution to the UNAM Genomics Team modeling, by proposing a mathematical model of their three component positive feedback network. | ||
| - | [ | + | '''We want to thank all the team members that answered our own survey which was about intellectual property. To see the results follow this [[Team:Mexico-UNAM-CINVESTAV/Human_Practices/Survey/Results | link]]'''. |
| + | |||
| + | |||
| + | ==Collaboration with [[Team:UNAM-Genomics_Mexico/Collaboration | UNAM Genomics Mexico]] == | ||
| + | |||
| + | <center>[[Image:Meeting.jpg|500px]]</center> | ||
| + | |||
| + | The system our countrymen asked us to model was a three element positive feedback loop. They expected us to find an oscillatory behaviour in time between the concentration of the three substances. | ||
| + | |||
| + | [[Image:Cliclo_Genomicas.png|center]] | ||
| + | |||
| + | *Cycle | ||
| + | *Positive Feedback | ||
| + | *Kind of Repressilator system | ||
| + | |||
| + | |||
| + | |||
| + | [[Image:Linear_Model.png]] | ||
| + | |||
| + | |||
| + | We proposed a linear model thinking in a first approach to solve the problem. | ||
| + | For each of the rate of change of the concentration in time there is a dependance with the substance itself and with one of the other substances. | ||
| + | These dependances are cyclic. | ||
| + | |||
| + | [[Image:First_version.png]] | ||
| + | |||
| + | [[Image:Sistema_Lineal1.png|center]] | ||
| + | |||
| + | The resulting dynamics of these equations are represented in the following images. | ||
| + | |||
| + | |||
| + | {| | ||
| + | | [[Image:Figura1_lineal.jpg|425px|none|thumb| y1(0)=1.5, y2(0)=1, y3(0)=1]] || [[Image:Figura2_lineal.jpg|425px|none|thumb|y1(0)=0, y2(0)=3, y3(0)=10]] | ||
| + | |- | ||
| + | | [[Image:Figura3_lineal.jpg|425px|none|thumb|y1(0)=1, y2(0)=10, y3(0)=1]] || [[Image:Figura4_lineal.jpg|425px|none|thumb|y1(0)=2.5, y2(0)=0.1, y3(0)=0.5]] | ||
| + | |} | ||
| + | |||
| + | [[Image:Sistema_LinealT2.png]] | ||
| + | [[Image:Sistema_Lineal2.png|center]] | ||
| + | |||
| + | |||
| + | The resulting dynamics of these equations are represented in the following images. | ||
| + | |||
| + | |||
| + | {| | ||
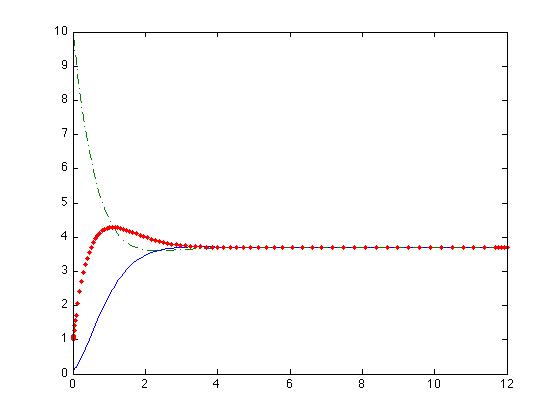
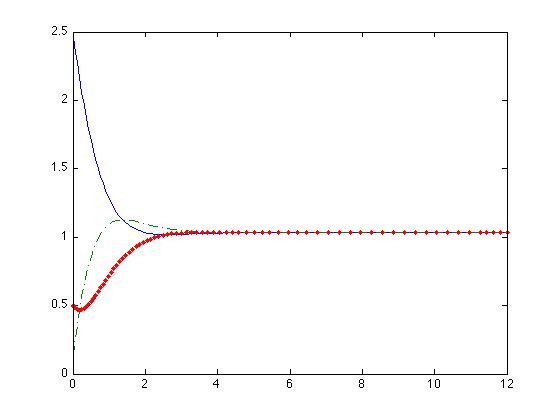
| + | | [[Image:Sistema_Lineal4.png|425px|none|thumb|r1=1 r2=1 z=4; y1 = y2 = y3 = 1; d1=3, d2=19, d3=17; u1(t)=39, u2(t)=-1, u3(t)=-1; y1(0)=0.1, y2(0)=0.2, y3(0)=0.8]] || [[Image:Sistema_Lineal3.png|425px|none|thumb|r1=1, r2=1, z=2; y1 = y2 = y3 = 1; d1=3, d2=4, d3=2; u1(t)=9, u2(t)=-1, u3(t)=-1; y1(0)=0.1, y2(0)=0.2, y3(0)=0.8]] | ||
| + | |- | ||
| + | | [[Image:Sistema_Lineal5.png|425px|none|thumb|r1=1 r2=1 z=2; y1 = y2 = y3 = 1; d1=3, d2=7, d3=5; u1(t)=15, u2(t)=-1, u3(t)=-1; y1(0)=0.1, y2(0)=0.2, y3(0)=0.8]] || | ||
| + | |} | ||
| + | |||
| + | In these images we observe that the system only posses an stable equilibrium point. | ||
| + | |||
| + | [[Image:Sistema_No_LinealT.png]] | ||
| + | |||
| + | By making the model a little more realistic we added another form of dependance of the substance concentration change in time. We also added a saturation term and a degradation term. | ||
| + | |||
| + | |||
| + | |||
| + | [[Image:Sistema_No_Lineal.png|center]] | ||
| + | |||
| + | |||
| + | |||
| + | Non Linear Simulation | ||
| + | |||
| + | |||
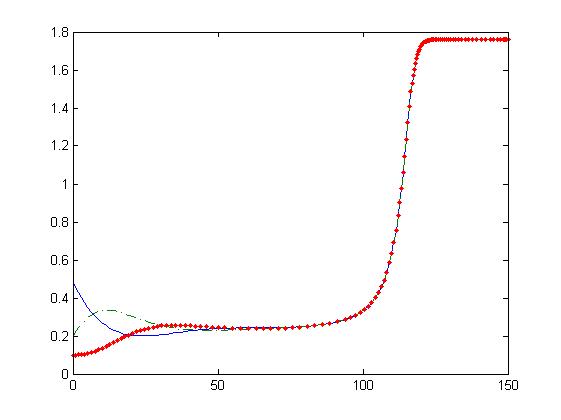
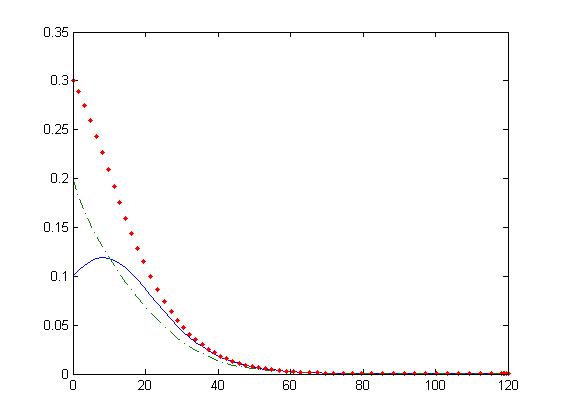
| + | In the following images we appreciate that there is a bifurcation point such that we obtain two different dynamics, one in which the system saturates and other in which the substances concentration reaches the zero value. | ||
| + | |||
| + | {| | ||
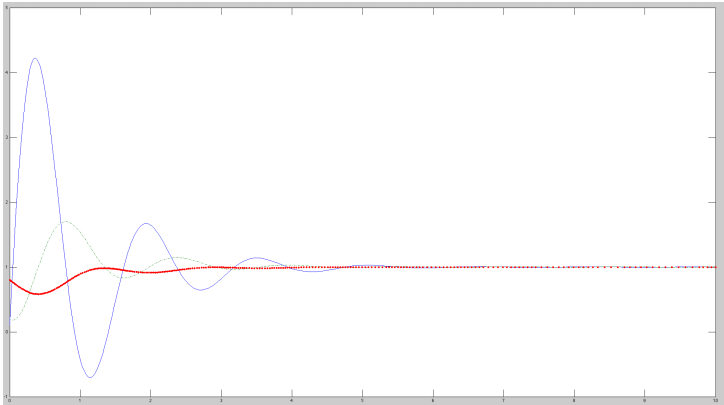
| + | | [[Image:Figura1_nolineal.jpg|425px|none|thumb| k1=k2=k3=0.5; M1=M2=M3=2; σ=-0.1045]] || [[Image:Figura2_nolineal.jpg|425px|none|thumb| k1=k2=k3=0.5; M1=M2=M3=2; σ=-0.1045]] | ||
| + | |- | ||
| + | | [[Image:Figura3_nolineal.jpg|425px|none|thumb| k1=k2=k3=0.5; M1=M2=M3=2; σ=-0.1045]] || | ||
| + | |} | ||
| + | |||
| + | |||
| + | ===Extension=== | ||
| + | |||
| + | With the two approaches above we did not obtained an oscillatory behavior as expected. Nevertheless, an idea emerged from the team. There could be an use for the dynamics we encountered. The idea was to 'reset' the system every certain amount of time. This 'pacemaker' system looks like this: | ||
| + | |||
| + | Pacemaker | ||
| + | |||
| + | [[Image:Pacemaker1.jpg|750px |center]] | ||
| + | |||
| + | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
{{Template:Mexico-UNAM-CINVESTAV-FOOTER}} | {{Template:Mexico-UNAM-CINVESTAV-FOOTER}} | ||
Latest revision as of 23:51, 27 October 2010
Participation in other surveys
This year we think was the most collaborative one. there were plenty of surveys, meetings and intense information exchange. Next we describe all the
Our team participated in different surveys:
- Warsaw Team
- METU_Turkey_Software Team
- University of Edimburg iGEM Team
We also made a contribution to the UNAM Genomics Team modeling, by proposing a mathematical model of their three component positive feedback network.
We want to thank all the team members that answered our own survey which was about intellectual property. To see the results follow this link.
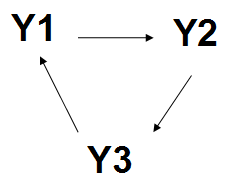
Collaboration with UNAM Genomics Mexico

The system our countrymen asked us to model was a three element positive feedback loop. They expected us to find an oscillatory behaviour in time between the concentration of the three substances.
- Cycle
- Positive Feedback
- Kind of Repressilator system
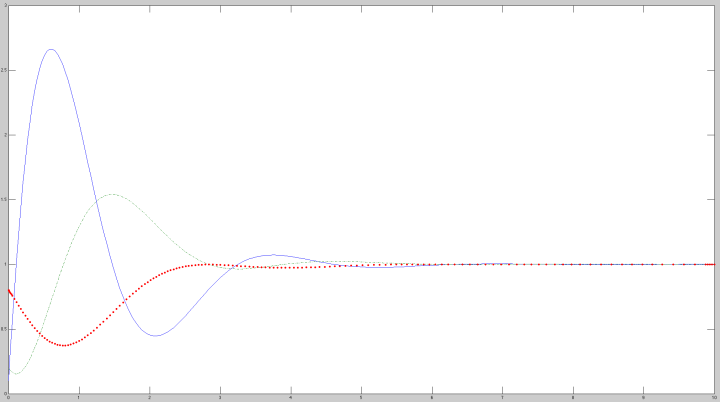
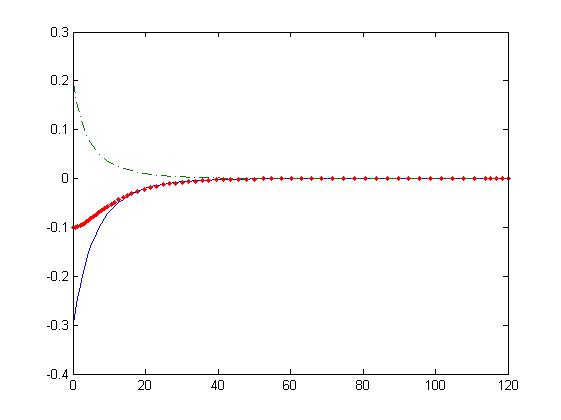
We proposed a linear model thinking in a first approach to solve the problem.
For each of the rate of change of the concentration in time there is a dependance with the substance itself and with one of the other substances.
These dependances are cyclic.
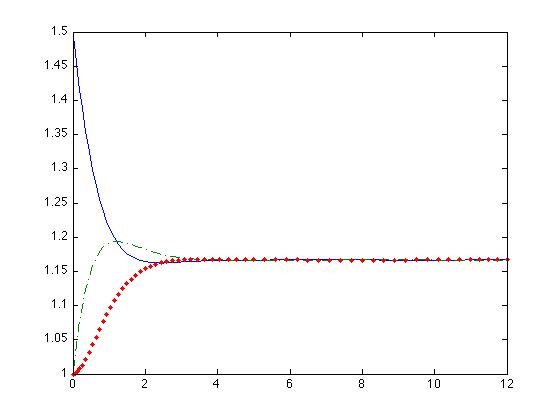
The resulting dynamics of these equations are represented in the following images.
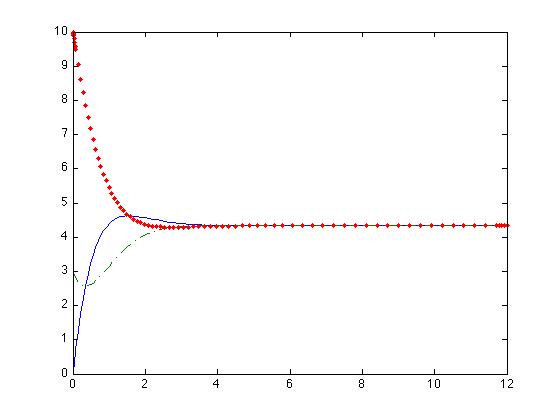
The resulting dynamics of these equations are represented in the following images.
In these images we observe that the system only posses an stable equilibrium point.
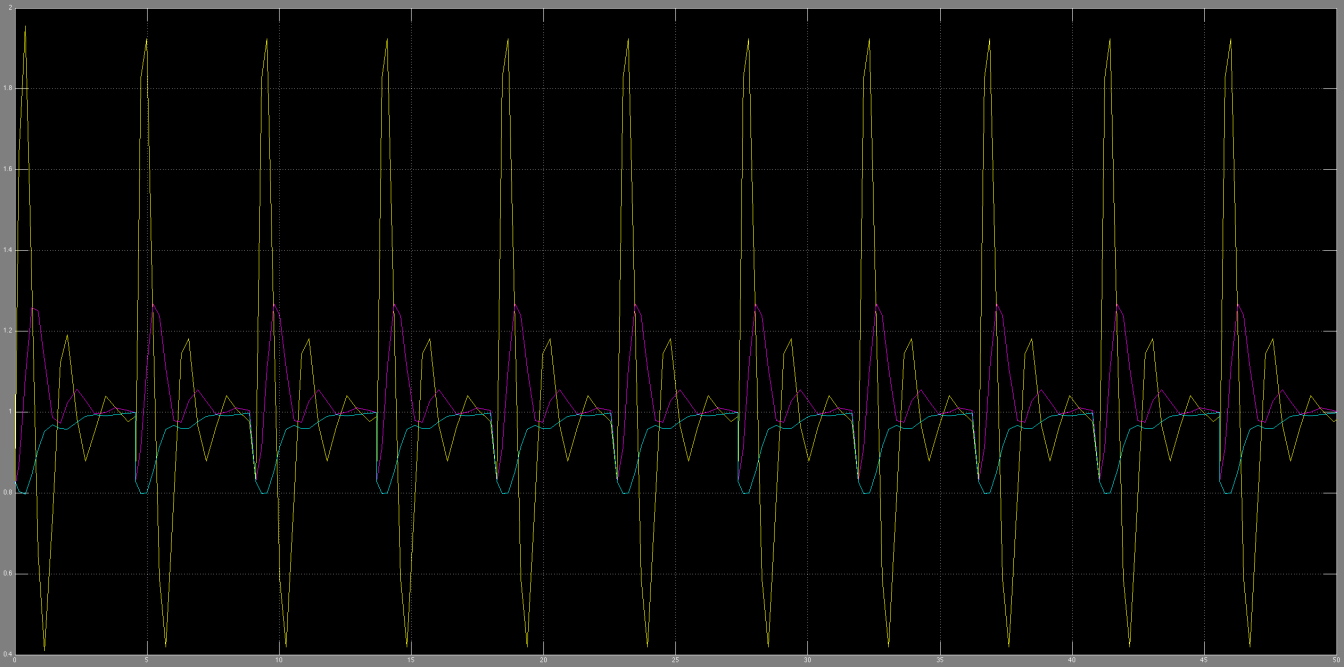
By making the model a little more realistic we added another form of dependance of the substance concentration change in time. We also added a saturation term and a degradation term.
Non Linear Simulation
In the following images we appreciate that there is a bifurcation point such that we obtain two different dynamics, one in which the system saturates and other in which the substances concentration reaches the zero value.
Extension
With the two approaches above we did not obtained an oscillatory behavior as expected. Nevertheless, an idea emerged from the team. There could be an use for the dynamics we encountered. The idea was to 'reset' the system every certain amount of time. This 'pacemaker' system looks like this:
Pacemaker
 |
 |
 |
 |
 "
"