Team:Heidelberg/Modeling/descriptions
From 2010.igem.org
(→Fuzzy Logic Model) |
|||
| Line 53: | Line 53: | ||
====Simulation and experimental verification==== | ====Simulation and experimental verification==== | ||
| - | ==Fuzzy Logic Model== | + | ==Fuzzy Inference Model== |
| + | ===Why using a fuzzy inference system to model binding site efficiency?=== | ||
| + | |||
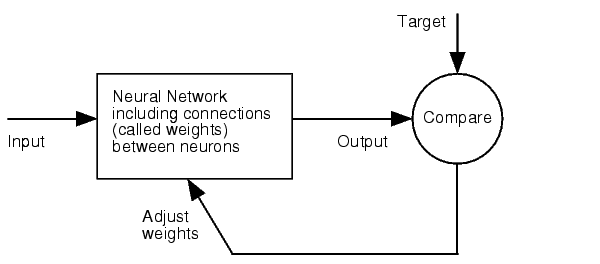
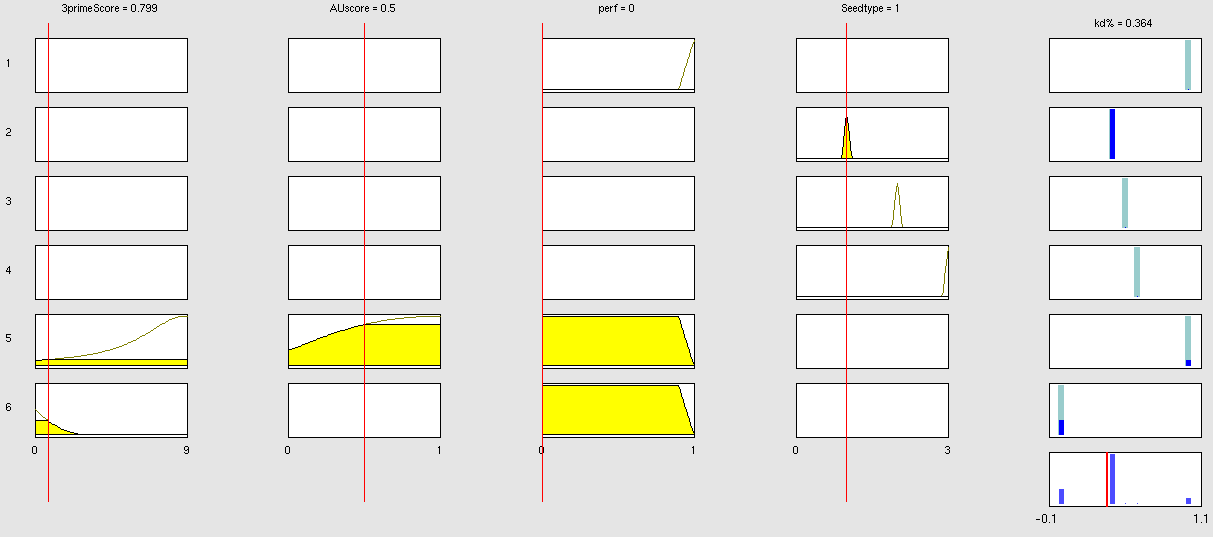
| + | To be able to evaluate the complex features of an shRNA or miRNA binding site and predict a resulting knockdown percentage of the protein we developed a fuzzy inference system (fis). The parameterized properties of the binding sites serve as input and will be processed into the knockdown percentage as the single output. Thus our fuzzy inference system is characterized as a multiple input, single output fuzzy inference system (MISO). | ||
| + | Fuzzy Logic is a rule-based approximate artificial reasoning method developed by Lotfi Zadeh in 1965. Its motivation is the observation that humans often think and communicate in a vague way, and yet can make precise decisions [Nelles O. Nonlinear System Identification Springer Verlag GmbH & Co., Berlin, 2000.]. It has been widely used in engineering and Artificial Intelligence approaches such as Fuzzy Controllers and Fuzzy Expert Systems. Fuzzy Logic has also been used for the modeling of biological pathways [Bosl W. J. Systems biology by the rules: hybrid intelligent systems for pathway modeling and discovery. BMC Systems Biology1:13 (2007).] and to analyze gene regulatory networks [Laschov D., Margaliot M. Mathematical modeling of the lambda switch:a fuzzy logic approach. J Theor Biol. 21:475-89 (2009)]. Key advantages of Fuzzy logic-based approaches are (i) the ability to construct models based on prior knowledge of the system and experimental data and (ii) encode intermediate states for inputs and outputs, thus improving other logic-approaches that can only deal with ON/OFF states such as Boolean models [Aldridge B. B., Saez-Rodriguez J., Muhlich J. L., Sorger P. K., Lauffenburger D. A. Fuzzy logic analysis of kinase pathway crosstalk in TNF/EGF/insulin-induced signaling PLoS Comput Biol.5:e1000340 (2009).] and (iii) simulations can be derived from both qualitative and quantitative data, both of which can be cast into the form of IF-THEN rules. Thus, FL constitutes a powerful approach for the understanding of heterogeneous datasets. | ||
| + | Fuzzy inference systems are based on membership functions (MF). MF rate input parameters on a scale from 0 to 1, how much they satisfy a criterion. There can be one, or multiple criteria – called membership function - for one input parameter. The height of persons for example can be evaluated with one MF - how much the person satisfies being tall. On the other hand, there could be 3 MFs, one evaluating the membership to small people, the second to medium sized people and the third one to big people (Figure MembershipFunction1.png). In case of a persons height of 1.8 meter the MF “big” would be satisfied to about 0.6 (Figure MembershipFunctionBig.png). Like this, all input is converted to membership values from 0 to 1. Changing the shape of the MF gives the opportunity to have either functional dependencies, allowing intermediate states of the membership values, or simple ON/OFF states, where the membership value can be only 0 or 1 (Figure MembershipONOFF.png). Thus different kinds of input parameters can be evaluated with a fuzzy inference system. For the simple height example model the age of the person could be taken as second input and evaluated by a MF that is 0 until the age of 18 and 1 for older persons. Thus the model would differentiate between young and grown-up persons. | ||
| + | |||
| + | Simple if-then rules can then be used to combine the input MF to an output MF. The satisfaction of a rule by an object (set of input parameters) is defined by the degree of membership of the object to the different MF. The higher the satisfaction of the rule, the higher is the membership to the output MF. | ||
| + | The output MF can be a function like the input MF. This is the case in Mamdani method fuzzy inference systems [Mamdani, E.H. and S. Assilian, "An experiment in linguistic synthesis with a fuzzy logic controller," International Journal of Man-Machine Studies, Vol. 7, No. 1, pp. 1-13, 1975.]. We are using a Sugeno method fuzzy inference system [Sugeno, M., Industrial applications of fuzzy control, Elsevier Science Pub. Co., 1985.], where the output MF is either a constant or a linear function depending on input parameters. The advantage of a Sugeno fuzzy inference system is, that it is computationally more efficient and easier to optimize or adapt due to the more simple output MF. Due to the non-intuitive combination of the 3'-pairing and AU-content score, our fuzzy inference system needs to be optimized computationally. | ||
| + | |||
| + | |||
| + | How is our fuzzy inference system optimized? | ||
| + | MISO Sugeno Fuzzy Network Model | ||
| + | |||
| + | Optimizable | ||
| + | |||
| + | Extendable | ||
| + | |||
| + | |||
| + | ===Fuzzy Model Concepts=== | ||
| + | |||
| + | |||
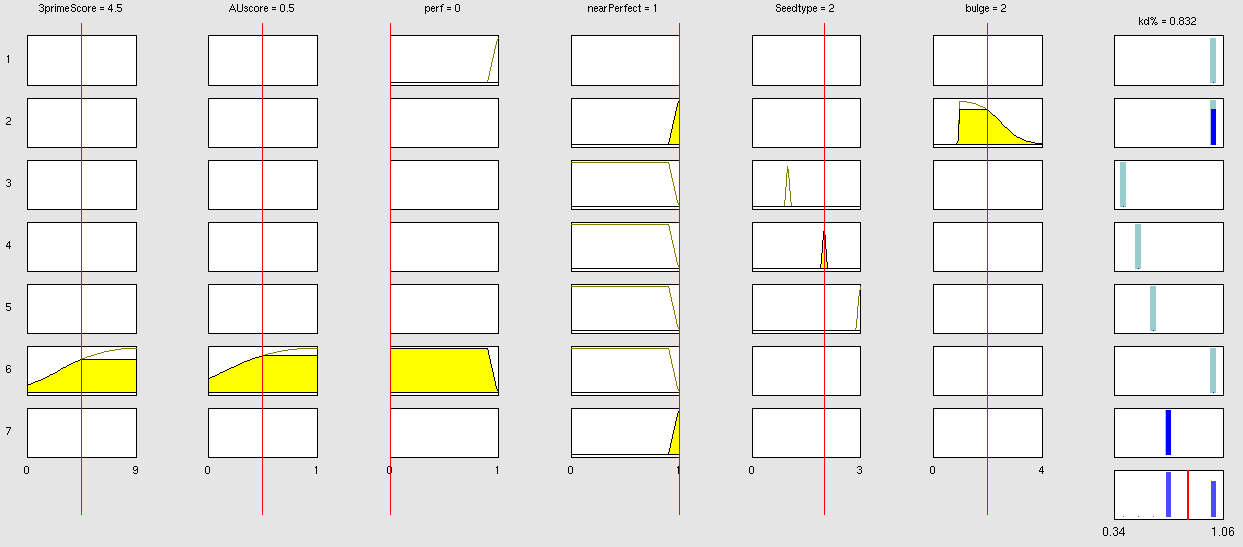
| + | [[Image:Nearperfect.png|thumb|Bulged binding sites concept: This model concept evaluates bulged- or "near-perfect" binding sites separately from conventional seed + 3'-pairing binding sites. Rule number 2 considers the bulge-size of the bulged binding site.]] | ||
| + | |||
| + | [[Image:BulgeAU.png|thumb|Bulged binding sites (including AU-content-score) concept: This concept extends the bulged-BS concept with the addition of AU-content score evaluation. Therefore rule number 2 was modified accordingly.]] | ||
| + | |||
| + | [[Image:LowthreePrime.png|thumb|Consider low 3' score concept: This model concept takes into consideration, that binding sites with a 3'-score under 3 did not show a significant change in knockdown efficiency compared to a control with only seed pairing {{HDref|Grimson et al., 2007}}. This is realized by rule number 6.]] | ||
| + | |||
| + | Strength: general prediction, no dependency on conditions. Assured by [normalization strategy] | ||
| + | |||
| + | based on previous knowledge [Bartel] | ||
| + | |||
| + | Our fuzzy inference system can deal with 3 different kinds of shRNA binding sites. Perfect, bulged and endogenous-like binding sites are treated separately, due to the differences in their biological mechanism, as discussed earlier [link to binding site properties]. | ||
| + | A perfect binding site is evaluated by a simple ON/OFF input MF evaluating the boolean input of | ||
| + | |||
| + | We came up with different concepts of what kind of input parameters to integrate into the fuzzy inference model and how to evaluate them. Therefore we parameterized the [https://2010.igem.org/Team:Heidelberg/Modeling/trainingset properties of a large set of binding sites] according to various different BS characteristics. | ||
| + | The targetscan_50_context_scores – Algorithm {{HDref|Rodriguez et al., 2007}} which evaluates binding sites in respect to 3'-pairing and AU-content gives out a score that seems appropriate to distinguish especially between endogenous miRNA like binding sites. A more detailed description on the concept of binding site parameterization can be found under [https://2010.igem.org/Team:Heidelberg/Modeling/trainingset Model Training Set]. | ||
| + | |||
| + | Input parameters | ||
| + | |||
| + | Input membership functions | ||
| + | |||
| + | Output membership functions | ||
| + | |||
| + | Rules | ||
| + | |||
| + | |||
| + | Optimization | ||
| + | |||
| + | Parameters and their functionality | ||
| + | |||
| + | Output Membership function values | ||
| + | |||
| + | 7merA1 | ||
| + | |||
| + | 7merM8 | ||
| + | |||
| + | 8mer | ||
| + | |||
| + | (Nearperfect) | ||
| + | |||
| + | (Perfect) | ||
| + | |||
| + | |||
| + | <html> | ||
| + | <div class="backtop"> | ||
| + | <a href="#top">↑</a> | ||
| + | </div> | ||
| + | </html> | ||
| + | ===Fuzzy Model Optimization=== | ||
| + | |||
| + | |||
| + | |||
| + | ===Result=== | ||
| + | |||
| + | [http://igem.bioquant.uni-heidelberg.de/igem_2010/FuzzyModelResults.html Click here, if you are interested in more recent model optimizations results!] | ||
==Training Set Overview== | ==Training Set Overview== | ||
Revision as of 21:48, 26 October 2010

|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 "
"