Team:BCCS-Bristol/Modelling/BSIM/Geometric Modelling/Implementation
From 2010.igem.org
(New page: {{:Team:BCCS-Bristol/Header}} ==Implementation== There are two computational structures that need to take account of complex three dimensional structures if these features are to be impl...) |
|||
| Line 12: | Line 12: | ||
object. Vertices are joined together into edges and these edges are joined together into faces. The | object. Vertices are joined together into edges and these edges are joined together into faces. The | ||
most primitive type of face is the triangle, which is the base face unit of all meshes. More complex | most primitive type of face is the triangle, which is the base face unit of all meshes. More complex | ||
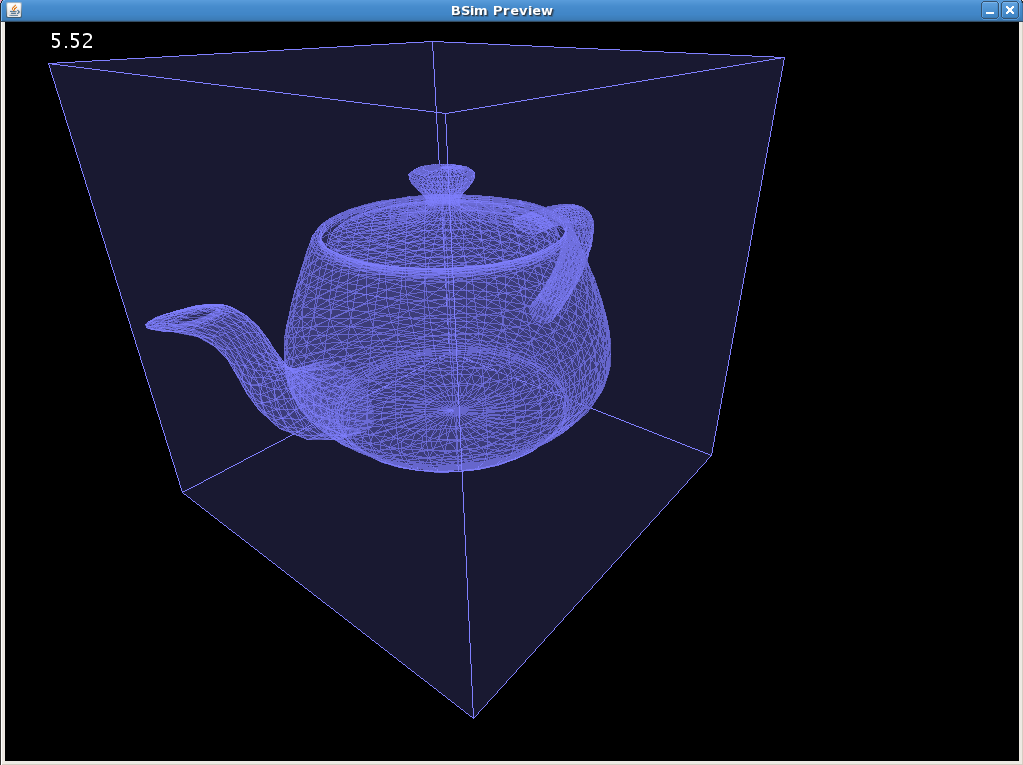
| - | shapes are made of many triangles, e.g. fig. | + | shapes are made of many triangles, e.g. fig. 1. Meshes can be imported from graphical modelling |
programs / image segmentation algorithms in the standard ‘.obj’ format, which specifies a list of | programs / image segmentation algorithms in the standard ‘.obj’ format, which specifies a list of | ||
vertices, edges, faces and normals that describe a given shape. | vertices, edges, faces and normals that describe a given shape. | ||
| - | The | + | [[Image:Teapot_Mesh.png|200px|thumb|left|fig 1]] |
| + | |||
| + | The diffusion of chemicals across the chemical field must be also computed. This involves | ||
solving a differential equation across an arbitrarily shaped 3D space. There are two broad classes | solving a differential equation across an arbitrarily shaped 3D space. There are two broad classes | ||
of methods that are used to do this, finite element methods and finite difference methods. | of methods that are used to do this, finite element methods and finite difference methods. | ||
| Line 26: | Line 28: | ||
a finite element method that works reliably in an arbitrary geometry without numerical instability. | a finite element method that works reliably in an arbitrary geometry without numerical instability. | ||
An example of a tessellation of triangles used to compute a finite element method approach can be | An example of a tessellation of triangles used to compute a finite element method approach can be | ||
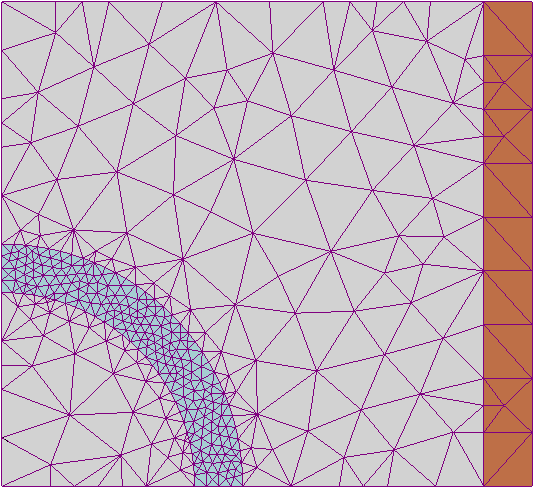
| - | seen in fig. | + | seen in fig. 2(a). An accurate finite element model would converge to the analytical solution as the |
mesh became finer and finer, unfortunately this is difficult to do in generality, such a model which | mesh became finer and finer, unfortunately this is difficult to do in generality, such a model which | ||
would be necessary for a robust addition to this modelling framework. | would be necessary for a robust addition to this modelling framework. | ||
A finite difference method discretizes and computes a differential equation over a regular lattice, | A finite difference method discretizes and computes a differential equation over a regular lattice, | ||
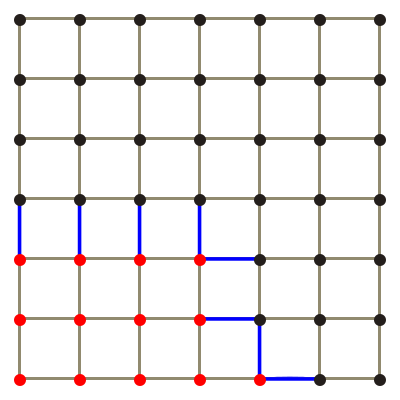
| - | e.g. fig. | + | e.g. fig. 2(b) This means that it is much more numerically stable than the finite element method. |
The trade-off is that you have to partition the space along the lines of this regular grid. Which is not | The trade-off is that you have to partition the space along the lines of this regular grid. Which is not | ||
a very accurate representation of curves unless the resolution of the lattice is very high compared | a very accurate representation of curves unless the resolution of the lattice is very high compared | ||
to the resolution of the curved object that you wanted to represent. | to the resolution of the curved object that you wanted to represent. | ||
| + | |||
| + | |||
| + | [[Image:FEM.png|200px|thumb|left|fig 2a]] | ||
| + | [[Image:FDM.png|200px|thumb|right|fig 2b]] | ||
| + | |||
The solution that we decided to use to implement the chemical field processing is an ‘octree’ | The solution that we decided to use to implement the chemical field processing is an ‘octree’ | ||
Revision as of 12:52, 26 October 2010
iGEM 2010
Implementation
There are two computational structures that need to take account of complex three dimensional structures if these features are to be implemented. One is the ability to represent a 3D shape inside the BSim environment, for example to provide a boundary, the other is the ability to represent a chemical field defined by such a 3D shape.
The choice as to how to represent a 3D shape was relatively straightforward, a polygon mesh is used. A polygon mesh is a collection of vertices, edges and faces that together define a polyhedral object. Vertices are joined together into edges and these edges are joined together into faces. The most primitive type of face is the triangle, which is the base face unit of all meshes. More complex shapes are made of many triangles, e.g. fig. 1. Meshes can be imported from graphical modelling programs / image segmentation algorithms in the standard ‘.obj’ format, which specifies a list of vertices, edges, faces and normals that describe a given shape.
The diffusion of chemicals across the chemical field must be also computed. This involves solving a differential equation across an arbitrarily shaped 3D space. There are two broad classes of methods that are used to do this, finite element methods and finite difference methods.
A finite element approach would use the mesh as a basis to generate a series of discrete units across which to calculate a discretized approximation system of ordinary differential equations. This is difficult to do reliably with arbitrary shapes. There exist several different algorithms that work well with different types of spaces (smooth, jagged, convex, concave) but it is difficult to implement a finite element method that works reliably in an arbitrary geometry without numerical instability. An example of a tessellation of triangles used to compute a finite element method approach can be seen in fig. 2(a). An accurate finite element model would converge to the analytical solution as the mesh became finer and finer, unfortunately this is difficult to do in generality, such a model which would be necessary for a robust addition to this modelling framework.
A finite difference method discretizes and computes a differential equation over a regular lattice, e.g. fig. 2(b) This means that it is much more numerically stable than the finite element method. The trade-off is that you have to partition the space along the lines of this regular grid. Which is not a very accurate representation of curves unless the resolution of the lattice is very high compared to the resolution of the curved object that you wanted to represent.
The solution that we decided to use to implement the chemical field processing is an ‘octree’
structure. This is a hybrid between the two methods, though is more closely related to the finite
difference method. This uses a regular lattice of cubes, but changes the resolution of the lattice
as it is partitioned by a mesh surface. This technique is visualized in fig. 10, note how the lattice
resolution increases around the sphere mesh, this allows for a more accurate division of the lattice
into a sphere shape. An octree structure will never be able to perfectly duplicate the shape of the
mesh that it is cast from, but the maximum resolution can be far higher than a regular lattice
with respect to its memory requirements because it only divides itself into a high resolution where
necessary.
 "
"