Team:USTC Software/projectModeling
From 2010.igem.org
Introduction of MoDeL based Automatic Modeling Algorithm
Development of Modeling Database Language (MoDeL) aims to provide a platform that enables separation of work between modeling and data constructing. Users could obtain dynamic behaviors of various quantities and other properties of a biological system as the output of iGame while they know nothing about details of modeling and the reaction network. Previous modeling and simulation tools require users to construct the network themselves, which is very hard even for professional researchers. iGame has no such requirements and users are only required to input data about the initial environmental condition of system. Hence, modeling is a task that is performed to find all reactions and species in the system.
To complete the final network from initial environment conditions, we first break up the task to several parts:
(1) Setup initial conditions and environmental parameters read from the input file.
(2) Species produced are inserted into a list in the order of time. For each species, we search the database to find template species which could be matched to this species in structural pattern. If not found, then go for the next species.
(3) For each template species we found, we continue to search template reactions containing this template species as a reactant or modifier or both. Only forward or reverse reaction is handled, never for both.
(4) For each template reaction found, we search in the species list for possible species which could be instances of templates of other reactants and modifiers. If not found, then go for next reaction.
(5) For each possible combination of reactants and modifiers, if the reaction parameter conditions are satisfied, we generate the structure of products based on the transfer table and structural templates of products. And then add this new reaction to the reaction list.
(6) Go to step 2 until the end of the species list.
In the following, we will focus on the step (2), (3) and (5). Our algorithms are totally different with that of other software tools since we design them for the purpose of proving the feasibility of MoDeL for synthetic biology. They are kind of complicated because the complexity of biological systems require so.
What are special reactions and How to handle with them?
Transcription and translation reactions are not supported by MoDeL reaction definitions; they are handled specially in the core program. We use pseudo first-order reaction to model both transcription and translation reactions (RNA polymerase are ignored). The rate constant k is the value of forwardPromoterEfficiency/reversePromoterEfficiency for transcriptions and forwardRbsEfficiency/reverseRbsEfficiency for translations defined for each part in the database. A transcription will not end at a terminator with termination efficiency less than 100% (values are stored in attribute forwardTerminatorEfficiency/reverseTerminatorEfficiency): RNA polymerase will pass over and continue transcription. For translation reactions, the prerequisite condition is that the part next to RBS along the 5' to 3' direction must have non-zero attribute value forwardStartCodon/reverseStartCodon. Opposite to transcriptions, translation reactions would stop if one part with non-zero attribute value forwardStopCodon/reverseStopCodon is encountered.
What are differences from single compartment to multi-compartment?
Consider an example first. AHL molecules outside diffuse into E.coli cells with rate k1, while AHL molecules inside E.coli cells diffuse outward and enter into the bio-reactor with rate k2. We assume diffusion reactions are all driven by concentration gradient.
Chain Sorting and Weighting Scheme
liaochen@mail.ustc.edu.cn
Chains in our Chain-Node Model should not have any order since there are no natural ways to sort them. One chain is not preferred to another, since in a complex of multiple chains, which are connected via binding interaction of binding bites on their own, all chains are equivalent. However, a chain-sorting program is a prerequisite for implementations of many other functions, such as comparison of two Chain-Node structures, or pattern matching of template species to those with definite structure.
Sorting is always performed under some rules. Since there are no natural options, we design one to generate the unique order for a list of chains. The rule we developed is something like that for comparing two strings: Compare first the partReference and partType defined in database of the first part of two chains in alphabet order and if equal, then compare the next until there are differences or the end of either chain. Meanwhile, a part in bound and unbound state(这里多了半句?)
If unicode_c of each chain is different with others, then we could sort the chain list by comparing their unicode_c (just the same with comparison of two strings). However, it is not always so: chains with same unicode_c may be equivalent or not. It is due to the mark asterisk *. Unicode_c knows where are the binding sites, but it does not know the binding details of that part. In other words, unicode_c could not solely determines the order of the chains since it lacks of information of the trees defined in our Chain-Node model. The forest (set of trees) in Chain-Node Model describes the binding details of parts in chains. We need to find something like unicode_c to represent the essence of the associated trees. Our weighting scheme will be first introduced below.
Assume the chains are sorted already. Each part will be assigned a weight based on its position in the chain list. The weight of the jth part on the ith chain is (i,j). For example, the first part on the first chain posses a weight (0,0) (in C style, counting number from zero). After assignment of parts' weight, we turn to weights of the nodes in trees. Since leaf nodes in trees are actually the representation of parts in bond state on chains, the weight of each leaf node could be inherited from the weight of its corresponding part. For parent node, its weight equals to the maximum of weights of all its children nodes (we define a weight (i, j) is greater than another (i',j') if i < i' or i = i' while j < j'). The recursive definition of tree nodes' weight make it possible to sort the forest. For convenience, we add a virtual node ROOT, whose weight value could also be obtained under the general rule, as the root of all trees in the forest and make a conversion from forest to tree. The tree structure could be uniquely determined by recursively sorting all children of each nodes by their weights.
Back to the question above, if two chains have the same unicode_c, which should be arranged ahead? The answer lies in the exchange of them. The exchange will change the parts' weight on both chains and thus the weight of some nodes of the trees. The tree structure (with virtual root) is also possible to change. If the tree structure is not changed, the two chains are equivalent, which means that it makes no difference to arrange either chain in front of the other. If the tree structure changes, we must find some ways to determine which tree structure is preferred and based on this to arrange the two chains with equal unicode_c. We know each tree could be uniquely converted to a binary tree by taking the first child of each node as the left child and its siblings as its right child. The Huffman algorithm could be used to generate the Huffman code of each node in the binary tree. Since the Huffman code is actually a representation of the path from current node to the root, we can restore the tree structure from the set of Huffman codes of all leaf nodes. Hence, the Huffman codes set of leaf nodes could uniquely represent a tree structure. We could generate a string, unicode_t for tree structure by splicing the Huffman codes and their weight of all leaf nodes sorted by their weights and adding a asterisk between two adjacent codes, for example:
[000:0:1][001:1:3][010:2:3][011:2:4]
Based on this idea, we could obtain the tree unicode_t for any possible order by exchanging equivalent chains and choose the order which make the minimum unicode_t value. By checking the unicode_t value of permutation, chains are grouped in a number of equivalent classes, which contains one or more chains. Chains within each equivalent classes are equivalent: exchanging order of any two chains will not change the tree structure.
It is easy to compare two Chain-Model structures with the help of chain sorting. We only need to compare unicode_c value of chains in the chain list and unicode_t value generated under that order. If two structures are equal, their chain list and tree structure must be equal since the chains order is unique in our chain sorting method. If two structures have same unicode_c value of each chain and unicode_t value, they must be same structures since we could uniquely generate a Chain-Node structure from the strings.
How to find species with specific structural pattern of a template one?
We assume that if a combination of species in the species list could be structurally matched to reactants and modifiers templates defined within a reaction, they are possible to react with each other in the way as the reaction template describes. Hence, it is important to find such matchings between species in the species list and template ones defined in the database. We will first give the basic idea and then some modifications.
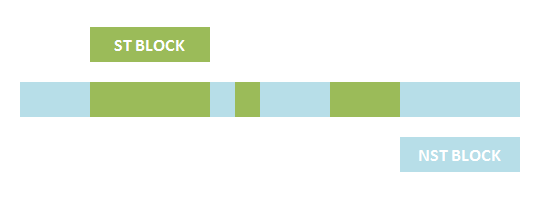
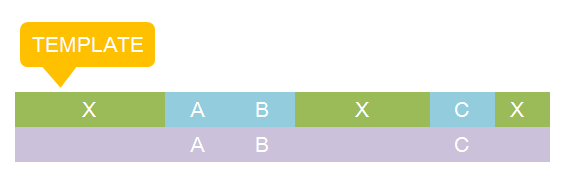
The basic idea is simple. We first consider the structural pattern matching between one chain and a chain template. There are two kind of parts on a chain template: substituent-type part (ST) and non-substituent-type part (NST). The whole template chain could be separated into blocks of ST parts and NST parts. Then we could break down the task to the matching of each small block. For each NST type block, we find all its matching regions on the chain to be matched, there may be more than one region. Each of the combinations of all NST blocks forms a NST frame and restricts the matching regions of ST blocks. Therefore, the minimal task is to find matchings of each ST part block within a restricted region on the chain to be matched. At the present version of MoDeL, there are 6 ST part: ANY, ANYUB, NZ, NZUB, ONE and ONEUB. A general algorithm for all 6 type part is designed and we will illustrate this via an example. Consider a ST block with all ANY type parts (we use X to indicate ANY type part in the figures). We find matchings of the first part of the block. There may be many possible matchings because part of type ANY implies arbitrary matching of parts on one chain in MoDeL definitions. For each matching found, we deal with the next, and do the same thing recursively until the end of the template or matching fails. An easy example is shown in the figure to illustrate this simple idea.
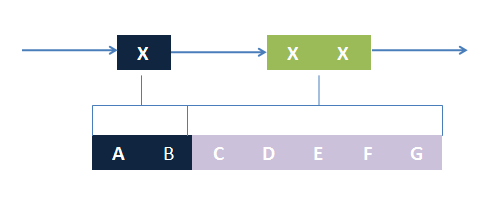
After all possible matchings for each chain in the template have been found, we could choose any one from each to form a combination. Matching alternatives of two different chains in the template should not be the same. For example, there are two chains in the template, T1 and T2, and three chains, C1, C2 and C3 in the species. If T1 has one matching to C1 and one to C2 and T2 has one to C2 and one to C3, the possible matchings are (T1,T2)->(C1, C2), (T1,T2)->(C1,C3) and (T1,T2)->(T2,T3). (T1,T2)->(C2,C2) is not allowed. (这里已修改)This is based on the assumption that the writer of template is always sure about the structure, he won't write a two-chain template if the parts are actually on one chain. The general matching relations could be written as (n1,n2,n3...)->(m1,m2,m3...), where (n1,n2,n3...) represents chains in the template and (m1,m2,m3...) represents the chains matched in the species for (n1,n2,n3...) respectively. However, it is only part of the matching relation because details, such as the matching positions of parts in the template, are ignored. The next question is: how to validate each matching?
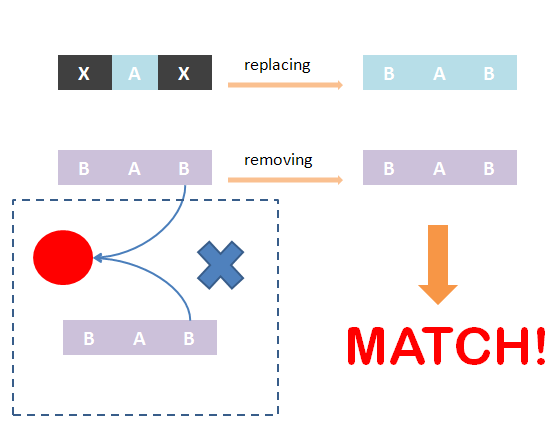
As defined in Chain-Node model, details of distribution of binding are stored in the forest. Matching of chains could not solely determine the overall match -- whether the template and the species have the same structural pattern. However, it is not easy to compare tree structure directly. We designed an algorithm to do this based on the principle: If the template and species have the same structural pattern, it must be possible to isolate the template from the species after replacing the ST part with its matchings. We first replace the ST part of the template with its matchings in the species. And then, we remove the chains which are not matched and the associated trees -- containing leaf nodes whose corresponding parts are on those chains. If the species after removing has the same Chain-Node structure with the template after replacing, the template and the species have the same structural pattern and in brief, the template could be matched to the species. We also illustrate this idea in figures.
However, there is one problem of this algorithm. Consider a LacI dimer template, whose Chain-Node model has two chains with one part on each and one tree with 2 leaf nodes. And there is also a LacI dimer species, it has the same structural pattern with the template. The matching should be (T1,T2)->(C1,C2) and (T1,T2)->(C2,C1) according to the algorithm described above. However, there is indeed one matching since the two matchings are the same. The underlying reason is that the two chains of the template are equivalent: it makes no difference to the tree structure (Huffman code of each node) if they are exchanged. Hence, several equivalent chains should be matched to a certain set of chains in the species only once.
How to create products based on database description?
In MoDeL frame, products are composed of both definite parts and ST parts. The sources of ST parts are defined in component listOfTransferTable. It seems to be very easy to generate Chain-Node structure of products from reactants and mod modifiers based on the transfer table. However, it doesn't.
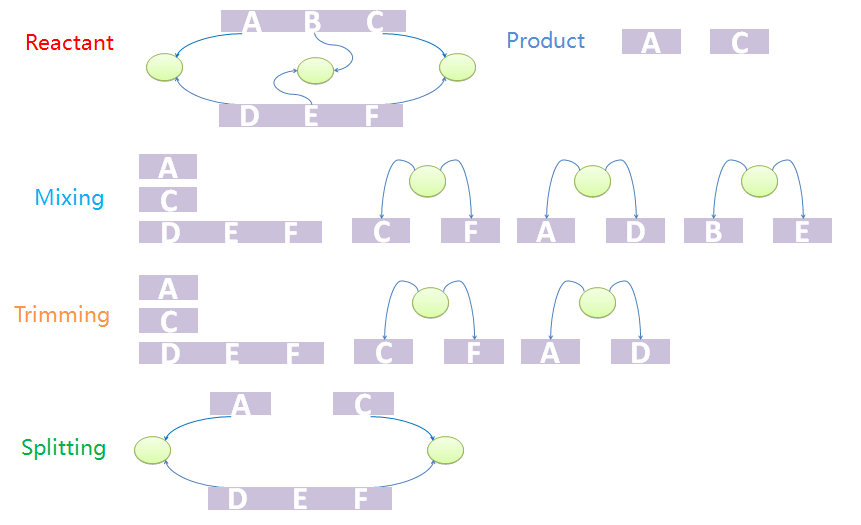
Consider first a template reaction with one reactant, A-B, where A and B are both NST parts. If it could be digested by a certain enzyme, the products should be A and B. In the real biological system, if there is a species with structure C-A-B-C, where the first part C and the last C binds to form a tree node. If we try to digest the A-B bond, the species would not be split into two pieces as expected because the two products as expected are connected by the tree node. To find products with correct structure, we design a three-step mix-trim-split algorithm to solve this problem.
The first step is to mix reactants and products. The mixture includes all chains of reactants except for those which are matched for some template chain as well as all trees. It also includes all chains and trees of products. And now we have a mixed species with chains and trees from different sources. It is worth noting that chains and trees of modifiers will not be added into the mixture. The next step is to trim the trees. Trees with leaf nodes that are not defined in chains will be removed from the forest. The last step is to split the products out from the mixture. This is because the mixture may not be one standalone complex. In other words, some chains that are not connected with others via tree nodes should not be incorporated into other species. The final standalone split species are real products in the system.
We provide an example to illustrate the product-generating procedure. The reactant has two chains, A-B-C and D-E-F. A, B, C bind with D, E, F, respectively. The products are A and C. First we mix chains and trees. Chain A-B-C will not appear in the mixture. Since node B does not appear in mixed chains, tree with nodes B and E will be removed in the trim process. Because part C and F, A and D, are both bound to nodes, the final product should contain A and B both after split processing.
In the example above, there is only one product finally though two product templates are defined in database. In this case, the corresponding reverse reaction would never be found because it fails to match two templates to only one species. This is a drawback of our MoDeL language -- it does not support description of intra-molecular reactions. If A and C could react as different parts of the product, the reverse reactions would not be lost. However, supporting intra-molecular reactions is one of our future plans for refinement of our MoDeL language.
 "
"